Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 351234567891011121314151617181920212223242526272829303132333436373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

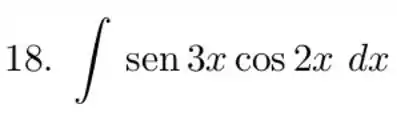
Passo 1

Para resolver essa integral precisamos saber uma formulinha que vai resolver o problema todo, anota aí

cos ⁡ t sen ⁡ s = sen ⁡ s + t + sen ⁡ s - t   2

Aplicando ao nosso caso

cos ⁡ 2 x sen ⁡ 3 x = s e n ⁡ ( 3 x + 2 x ) 2 + sen ⁡ 3 x - 2 x 2

cos ⁡ 2 x sen ⁡ 3 x = s e n ⁡ ( 5 x ) 2 + sen ⁡ x 2

Passo 2

Agora fazendo a integral

∫ cos ⁡ 2 x sen ⁡ 3 x   d x = 1 2 ∫ sen ⁡ ( 5 x )   d x + 1 2 ∫ sen ⁡ ( x )   d x

Para resolver

∫ sen ⁡ ( 5 x )   d x

Vamos fazer a seguinte substituição

u = 5 x

d u = 5   d x

Então ficamos com

∫ sen ⁡ 5 x   d x = 1 10 ∫ sen ⁡ ( u )   d u  

∫ sen ⁡ 5 x   d x = - 1 10 cos ⁡ ( u )

Desfazendo a substituição

∫ sen ⁡ 5 x   d x = - 1 10 cos ⁡ ( 5 x )

Aplicando lá na nossa integral maior

∫ cos ⁡ 2 x sen ⁡ 3 x   d x = 1 2 ∫ sen ⁡ ( 5 x )   d x + 1 2 ∫ sen ⁡ ( x )   d x

∫ cos ⁡ 2 x sen ⁡ 3 x   d x = - 1 10 cos ⁡ ( 5 x ) + 1 2 ∫ sen ⁡ ( x )   d x

Passo 3

Sabemos que

∫ sen ⁡ x   d x = - cos ⁡ x

Então

∫ cos ⁡ 2 x sen ⁡ 3 x   d x = - 1 10 cos ⁡ 5 x - 1 2 cos ⁡ x + C

Resposta

∫ cos ⁡ 2 x sen ⁡ 3 x   d x = - 1 10 cos ⁡ 5 x - 1 2 cos ⁡ x + C

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x