UFSC – Cálculo 1 – Lista 4.8 – Questão 1h
Calcule as integrais abaixo.
Passo 1
E aí pessoal, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! O problema pediu para calcularmos essa integral indefinida:
Como temos um integrando com senos e cossenos com potência PAR não tem mágica: precisamos usar a identidade trigonométrica para termos apenas uma função no integrando!
A relação fundamental da trigonometria é
Ficamos com essas duas integrais para resolver! Essa é nossa missão a partir de agora!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos começar resolvendo essa aqui:
Como a potência do cosseno é par, precisamos usar a técnica de integração por partes! Vamos separar em uma multiplicação de cossenos, uma parte será nosso e o restante nosso , de forma que o possa ser integrado:
Beleza?
Relembrando da fórmula da integração por partes
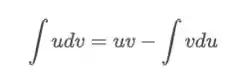vamos substituir:
E aqui quero sua atenção: essa questão pertence a lista 4.8, então se você está resolvendo em ordem já viu essa integral aí que surgiu na direita!
Mas estou aqui para ajudar quem caiu de paraquedas também! Então vou lá na lista 4.8 item (g) e resgatar o resultado:
Aqui foi usado essas identidades trigonométricas:
E mais uma dica: usamos a do cosseno duas vezes! E depois integramos! Se você não conseguir resolver, dá uma espiadinha na questão (g) da lista 4.8!
VOLTANDO para nossa integral:
E usando o resultado da integral à direita:
Tranquilo até aqui?
Passo 3
Agora vamos resolver a outra integral, então do passo 1:
A estratégia é: usar as identidades trigonométricas! A do cosseno ao quadrado nós já vimos:
E elevando ao cubo esse valor temos:
E podemos aplicar a mesma identidade naquele :
Simplificando temos:
Beleza?
Vamos integrar tudo que for possível agora:
E em um passo separado vou fazer essa integral ali! Bora?
Passo 4
Precisamos resolver essa integral:
Como comentei antes a estratégia aqui é: rescrever essa potência ímpar do cosseno deixando um cosseno e o resto substituir por , que vem da relação fundamental:
Daí nosso integrando fica assim:
Tranquilo até aqui?
E agora vamos integrar!
Fazendo a substituição :
Agora é só substituir:
E retornando para :
Beleza? Vamos substituir esse resultado na integral do passo anterior?
Estamos quase lá! Agora é só reunir os resultados!
Passo 5
Precisamos resolver essas integrais aqui:
No passo 2 resolvemos a primeira:
E no passo 4 a segunda:
Agora é só reunir os resultados:
Podemos agrupar os termos semelhantes:
Não esquece de colocar aquele no final!
E é isso!
Espero ter ajudado! Vamos para a próxima?