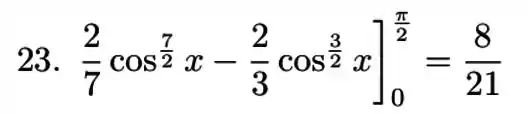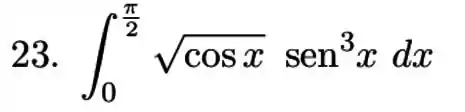
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 471234567891011121314151617181920212223242526272829303132333435363738394041424344454648495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos primeiro reescrever a nossa integral

∫ 0 π / 2 cos ⁡ x sen 3 ⁡ x   d x = ∫ 0 π / 2 cos ⁡ x sen 2 ⁡ x sen ⁡ x   d x

Agora, podemos usar a identidade trigonométrica sen 2 ⁡ x = 1 - cos 2 ⁡ x

∫ 0 π / 2 cos ⁡ x sen 3 ⁡ x   d x = ∫ 0 π / 2 cos ⁡ x ( 1 - cos 2 ⁡ x ) sen ⁡ x   d x

Passo 2

Beleza! Agora vamos usar a técnica da substituição para resolver

u = cos ⁡ x

d u = - sen ⁡ x   d x

Então ficamos com

∫ 0 π / 2 cos ⁡ x sen 3 ⁡ x   d x = - ∫ 1 0 u ( 1 - u 2 )   d x

∫ 0 π / 2 cos ⁡ x sen 3 ⁡ x   d x = ∫ 1 0 u   d u - ∫ 1 0 u 5 / 2   d u

∫ 0 π / 2 cos ⁡ x sen 3 ⁡ x   d x = - 2 3 u 3 / 2 1 0 + 2 7 u 7 / 2 1 0

Refazendo a substituição, e voltando pros limites de integração originais:

∫ 0 π / 2 cos ⁡ x sen 3 ⁡ x   d x = - 2 3 cos 3 / 2 ⁡ x   0 π / 2 + 2 7 cos 7 / 2 ⁡ x 0 π / 2

Aplicando os limites de integração

∫ 0 π / 2 cos ⁡ x sen 3 ⁡ x   d x = - 0 + 2 3 + 0 - 2 7 = 8 21

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x