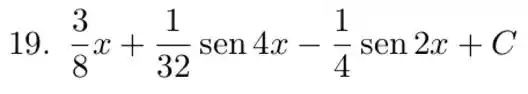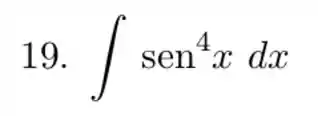
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 771234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757678798081828384858687888990919293949596979899100

Enunciado

Passo 1

Pra começar vamos fazer algumas manipulações na nossa integral

∫ sen 4 ⁡ x d x =   ∫ sen 2 ⁡ x 2 d x

Passo 2

Precisamos lembrar que

sen 2 ⁡ x = 1 - cos ⁡ 2 x 2

Então

sen 2 ⁡ x 2 = 1 - cos ⁡ 2 x 2 2

( sen 2 ⁡ x ) 2 = 1 - 2 cos ⁡ 2 x + cos 2 ⁡ 2 x 4

Passo 3

Com isso, podemos dividir nossa integral em 3 que já conhecemos

∫ sen 4 ⁡ x d x = ∫ 1 4 d x + ∫ - 2 4 cos ⁡ 2 x d x + ∫ cos 2 ⁡ 2 x 4 d x

∫ sen 4 ⁡ x d x = 1 4 ∫ d x - 1 4 ∫ 2 cos ⁡ 2 x d x + 1 4 ∫ cos 2 ⁡ ( 2 x ) d x

Passo 4

Precisamos fazer mais uma substituição, pra facilitar nossa vida

cos 2 ⁡ 2 x = 1 + cos ⁡ 4 x 2

Então nossa integral fica

∫ sen 4 ⁡ x d x = 1 4 ∫ d x - 1 4 ∫ 2 cos ⁡ 2 x d x + 1 4 ∫ 1 2 d x + ∫ cos ⁡ 4 x 2 d x

E resolvendo as integrais teremos

∫ sen 4 ⁡ x d x = 1 4 x - 1 4 sen ⁡ 2 x + 1 4 1 2 x + 1 8 sen ⁡ 4 x

∫ sen 4 ⁡ x d x = 1 4 x - 1 4 sen ⁡ 2 x + 1 8 x + 1 32 sen ⁡ 4 x

∫ sen 4 ⁡ x d x = 3 8 x - 1 4 sen ⁡ 2 x + 1 32 sen ⁡ 4 x + C

Não esqueça de colocar a constante de integração no final!

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x