Considere um projétil arremessado da origem no nível do solo ( e ) com velocidade inicial como descrito na figura.

Dados:

a) Utilizando as equações horárias para e , mostre que

b) Encontre a distância percorrida no eixo até o instante onde a partícula retorna ao solo (não substitua a gravidade ).

Existe uma parede na posição , com um buraco localizado a uma altura com espaço suficiente para que o projétil o atravesse. Você pode utilizar o resultado dos itens anteriores. Considere que a gravidade é .

c) Encontre para que o projétil atravesse o buraco.

A única aceleração atuando sobre o projétil é uma aceleração na vertical para baixo (gravidade ), então, ele vai realizar um movimento uniformemente acelerado nessa direção.

Enquanto isso, na horizontal o projétil irá manter sua velocidade constante, realizando um movimento uniforme.

Começando com o eixo , podemos utilizar a equação de movimento para um movimento uniforme:

Como o projétil parte da origem, sua posição inicial é zero. Além disso, sua velocidade na horizontal é a componente da velocidade em :

Já para o eixo , vamos utilizar a equação de movimento de um MUV:

Novamente a posição inicial é zero, já que parte da origem. A velocidade inicial é a componente em do vetor velocidade e a aceleração é a da gravidade, porém com o sinal negativo já que aponta para baixo :

Beleza, já temos as equações de movimento nos dois eixos.

Agora, queremos relacionar as duas coordenadas e .

Como a expressão que queremos chegar não depende do tempo , uma boa saída é substituir exatamente esse parâmetro de uma para outra, porque assim ele sumirá da expressão.

Na primeira temos:

Substituindo na segunda:

Letra (a), check!

Na letra (b), queremos a distância em até o projétil atingir novamente o chão, ou seja, o alcance na horizontal do projétil.

Bom, nesse tipo de situação, geralmente descobrimos primeiro o tempo em que leva até o projétil voltar ao solo e depois descobrimos o quanto ele andou em durante esse tempo.

Mas pensa comigo... acabamos de relacionar essas duas coordenadas com a expressão:

Então, podemos simplesmente substituir a coordenada por zero e descobrir em qual posição de isso acontece.

Achando as raízes da expressão:

Como temos um produto resultando em zero, um dos termos multiplicados tem que ser nulo.

Então, ou:

Ou:

Substituindo o valor de , temos:

Mas por que achamos dois valores para ?

Isso porque no início do movimento, o projétil também se encontra na altura do solo, porém, é o segundo valor que nos interessa, então, ficamos com:

Na letra (c), temos um buraco na parede que se encontra em:

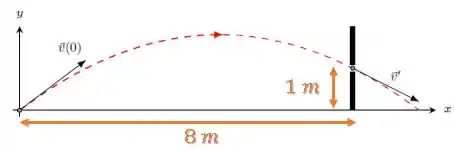
Queremos achar a velocidade para que o projétil passe por esse buraco.

Então, basicamente, precisamos substituir essas coordenadas na expressão que relaciona a coordenada com a coordenada :

E achamos que para que o projétil passe pelo buraco deve ser:

OBS: A unidade de será em pois colocamos os valores de posição em e o de aceleração em . Ou seja, todas as unidades estão no Sistema Internacional, assim como estará.