Durante uma experiência em um laboratório de Física, um professor simula o lançamento de um projétil por um tanque de guerra, com velocidade e com um ângulo de lançamento em relação à horizontal. Sendo , e . Sabendo-se que durante o experimento o professor desprezou a resistência do ar, podemos afirmar que a altura máxima do projétil medida pela simulação foi
(a)
(b)
(c)
(d)
(e)
Passo 1
Vamos fazer um desenho e colocar as informações que ele fala pra gente:
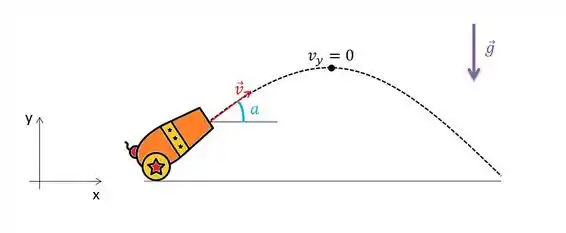
No ponto mais alto da trajetória temos que a componente da velocidade é zero. Pois se é o ponto mais alto, o projétil já subiu tudo o que podia subir, aí ele para, momentaneamente, e começa a descer. Ok?
Queremos a altura máxima que ele atinge, e sabemos que na direção vertical é um Movimento Uniformemente Variado, já que temos a aceletação da gravidade:
O menos é porque a gravidade aponta para baixo em relação a nossa referência.
Então, uma das equações para o MUV é a equação de torriceli, etão vamos aplicar ela da direção vertical:
Beleza?
Agora é só a gente achar o deslocamento em que achamos a altura máxima!
Acompanha aqui comigo.
Passo 2
O ângulo entre a velocidade inicial e a horizontal é , então as componentes e da velocidade inicial são:
Ele dá os valores da velocidade inicial e do ângulo, então:
Como falamos antes, no ponto mais alto a velocidade é zero. E a aceleração em é . Então vamos substituir tudo na equação de torricelli:
Arrumando isso daí:
 Uhuuul!!
Uhuuul!!
Resposta
Alternativa (a)