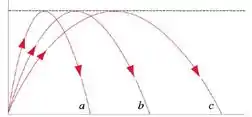
A figura mostra as trajetórias de três bolas de futebol que foram chutadas. Ignore a resistência do ar e considere as seguintes afirmações:
(I) o tempo de voo é o mesmo para todas as trajetórias;
(II) a trajetória corresponde à maior componente vertical da velocidade no lançamento;
(III) a componente vertical da velocidade no lançamento é a mesma para todas as trajetórias;
(IV) o módulo de velocidade de lançamento é o maior de todos para a trajetória ;
(V) o módulo de velocidade de lançamento é o maior de todos para a trajetória
São verdadeiras as afirmações:
(A) I, III e IV
(B) II e V
(C) I, III e V
(D) II e IV
(E) III e V
Passo 1
Analisando as afirmativas I, II e III
Como as três bolas alcançam a mesma altura máxima, encontraremos o valor da altura em função da velocidade (eixo Y).
Analisando o eixo Y.
Pela equação de Torricelli, temos:
No ponto mais alto:
Logo, a altura máxima só depende da velocidade inicial no eixo Y.
Como as alturas máximas são iguais, a componente vertical inicial das velocidades é a mesma para cada uma das bolas.
(Afirmativa III – Verdadeira / Afirmativa II – Falsa)
Calculando o tempo de subida (eixo Y):
Da equação da velocidade do MUV, temos:
Sendo a gravidade a aceleração da bola no eixo Y e sabendo também que no ponto mais alto a velocidade é nula, temos:
Como o tempo de subida é o mesmo que o tempo de decida, o tempo total de movimento:
Como a é a mesma para todas as bolas, o tempo de voo é o mesmo para todas as bolas. (Afirmativa I – Verdadeira)
Passo 2
Analisando as afirmativas IV e V.
Sendo a velocidade de lançamento da bola e o ângulo que a velocidade faz com a horizontal, podemos dizer que:
Como é o mesmo para todas as bolas e sabendo que aumenta com o aumento do ângulo , teremos que quanto maior o ângulo, menor o módulo da velocidade de lançamento e quanto menor o ângulo, maior o módulo da velocidade lançamento.
Da imagem, conseguimos observar que o ângulo de lançamento da bola é o menor entre todas as bolas, logo
(Afirmativa IV – Verdadeira / Afirmativa V – Falsa)