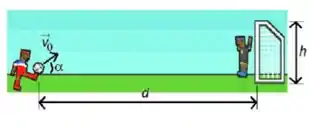
Um jogador de futebol chuta a bola de modo que o vetor velocidade inicial, , forma um ângulo com a direção horizontal. Despreze a resistência do ar e considere que a bola não sofre ação de outras forças além do campo gravitacional.
Considere , e
a) Suponha que e . Determine o módulo do vetor velocidade da bola, , para que a bola atinja a trave superior do gol.
b) Calcule o vetor velocidade em .
c) Calcule o instante de tempo em que a bola atinge a altura máxima.
d) Ao atingir a trave, a bola estava subindo ou descendo? Explique.
Passo 1
Bom, pelo modo que ele vai chutar a bolinha, deu pra ver que é questão de lançamento oblíquo, certo?
Então, vamos primeiro montar as equações de movimento nos dois eixos: e .
A velocidade inicial pode ser decomposta da seguinte forma:
Como só vai ter aceleração no eixo , as equações vão ficar assim:
Substituindo os valores temos:
Passo 2
Letra a)
Como ele nos deu os valores de e em um mesmo tempo, podemos substituir os valores e vamos ficar com duas variáveis, o tempo e a velocidade.
Como nós queremos a velocidade, é só isolar o tempo.
Substituindo o tempo na equação do eixo e substituindo o pela altura dada ficamos com:
Substituindo os valores, temos:
Isolando aquele ali chegamos na velocidade que queríamos!
Passo 3
Letra b)
Como no eixo não temos aceleração, a velocidade fica constante ao longo de todo o movimento.
Já no eixo , vamos ter aceleração, então vamos precisar calcular certinho:
Logo o vetor velocidade vai ser dado por:
Passo 4
Letra c)
O instante que a altura é máxima é quando a velocidade é zero. Lembra que a gente viu isso na teoria? Qualquer coisa dá um pulinho lá pra relembrar.
Vamos usar aquela mesma equação da velocidade que usamos na letra anterior.
Passo 5
Letra d)
Bom, a gente sabe que quando a bola passa da altura máxima, ela começa a descer.
Agora é só descobrir o tempo em que a bola bateu na trave e ver se está antes ou depois do tempo da altura máxima.