Um jogador de futebol quer lançar a bola para ele mesmo, de forma que ela encubra os adversários e ele a recupere mais à frente. Considerando que a altura máxima do lançamento é de , e a velocidade máxima do jogador é de , que distância ele vai percorrer até recuperar a bola?

(a)

(b)

(c)

(d)

(e)

Dados:

Dá uma olhada aqui:

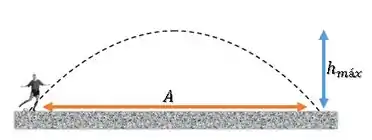
A questão não especifica exatamente como é o movimento do jogador, mas diz que sua velocidade máxima é . Então, vamos considerar que ele corre sempre com essa velocidade.

Assim, podemos usar a equação de um movimento retilíneo uniforme:

Considerando que sua posição inicial é zero , temos que o alcance vai ser:

Onde a velocidade é :

Então só falta achar o tempo para encontrar o nosso alcance .

Mas agora, como vamos achar esse tempo?

Para achar o tempo, vamos analisar o movimento vertical da bola.

Em um lançamento oblíquo, onde a bolinha vai e volta do chão até uma altura , lembra que o tempo de subida é igual ao tempo de descida ?

Então, o tempo de vôo que queremos encontrar é duas vezes o tempo de subida ou de descida:

Com isso, basta calcular ou e correr para o abraço.

Vamos calcular o tempo de descida , já que na descida é como se a bola realizasse uma queda livre, então as contas ficam mais simples. Sua posição pode ser escrita assim:

Na queda livre, temos a velocidade inicial nula , vamos considerar sua posição inicial como e a aceleração da gravidade negativa já que aponta para baixo:

Quando a bola chega ao chão, . Além disso, o valor da gravidade é :

Achamos o tempo de descida da bola. Então, o tempo total de vôo vai ser:

Agora que já sabemos o tempo, podemos finalmente substituir na equação do movimento do jogador e encontrar o alcance :

Ou seja, conseguimos a distância que o jogador vai percorrer até recuperar a bola.

Assim, achamos a altenativa (a).