Em um lançamento oblíquo sem resistência do ar, é correto afirmar que:
- A aceleração no topo da trajetória é zero.
- O movimento horizontal do projétil é uniformemente acelerado.
- O projétil tem aceleração constante no eixo vertical.
- A velocidade total na altura máxima é zero.
- O alcance máximo do lançamento se dá com um ângulo diferente de 45 graus.
Passo 1
Em um lançamento oblíquo, sem resistência do ar, durante todo o percurso de determinado projétil, só uma força vai estar atuando, beleza? E quem será ela se não a força peso? Dá uma olhada no esquema de um lançamento oblíquo:
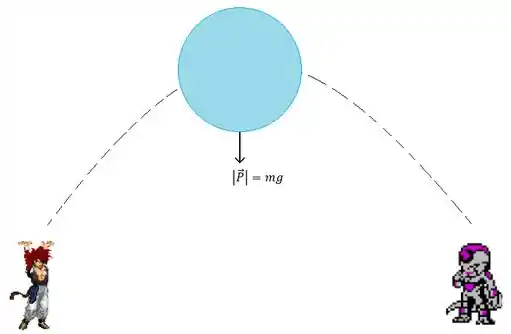
Se a força peso não para de atuar, então não tem como a aceleração do projétil ser zero em nenhum ponto da trajetória, não é mesmo? Sempre vai existir aceleração e ela será a aceleração da gravidade! Então nisso já descartamos a letra e já temos a resposta correta, a letra .
Mas pera, porque não pode ser a , ou ? Calma, vamos ver cada caso! Pra começar, olha bem pro projétil da figura: o que acontece com ele na horizontal? Tá vendo que não tem forças? Opa, sem forças resultantes, não tem como o corpo se acelerar horizontalmente! Logo ou ele está à velocidade constante ou parado, mas agora que estamos espertos não podemos marcar a letra por causa disso!
Agora, presta bastante atenção na letra : ele diz velocidade total! Ora, se o projétil está se movendo com velocidade constante na horizontal, mesmo que na vertical, em altura máxima, a velocidade seja zero, a velocidade total não tem como ser, não é mesmo? Até porque a velocidade total depende dessas duas componentes.
Pra fechar com chave de ouro, vamos fazer umas continhas pra ver a letra . Seja:
A gente pode usar essa equação tanto na horizontal quanto na vertical. Vamos olhar primeiro na vertical, beleza? Considerando o ponto inicial e o final como o chão, a gente pode achar o tempo de queda do projétil da seguinte forma:
Agora, na horizontal, como não temos aceleração, a fórmula vai ganhar uma nova cara, dá uma olhada:
Como o tempo que o projétil demora pra cair é o tempo que ele demora pra percorrer seu alcance, vamos juntar os dois resultados? Partiu então:
Tá, mas e daí? A letra fala de ângulos e na fórmula acima não tem nenhum! Calma! A gente consegue por sim ângulos na fórmula do alcance se lembrarmos que as componentes e do vetor velocidade inicial nada mais são do que o produto entre o módulo da velocidade inicial total vezes o cosseno e o seno, respectivamente, que essa velocidade faz com a horizontal. Então repaginamos o resultado anterior e conseguimos essa expressão simpática:
Se plotássemos a função , teríamos a seguinte curva:
Perai, quer dizer que quando essa função é máxima, vamos ter alcance máximo também? Exatamente! E veja que o ângulo que maximiza essa função são múltiplos positivos de . Então nossa letra não vai poder ser a correta.