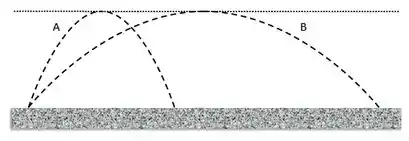
Vemos na figura duas trajetória distintas, descrevendo o movimento de dois projéteis lançados a partir do mesmo ponto, atingindo a mesma altura. Se avaliarmos a relação entre os tempos de voo, desprezando o efeito da resistência do ar, podemos dizer que:

(a) .

(b) .

(c)

(d)

(e) faltam dados para avaliar a relação entre os tempos de voo.

A questão se trata de um lançamento oblíquo.

Lembra que a gente pode analisar os movimentos na vertical e na horizontal separadamente?

Então, vamos lá. Olhando primeiro na horizontal, dá pra ver que as velocidades de e são diferentes.

Porém, isso não importa!

Ué, mas por que não?

Não importa porque a questão é apenas sobre o tempo de vôo dos projéteis, ou seja o tempo que eles ficam no ar.

Bom, e esse tempo vai depender apenas da altura, pois o movimento na vertical é independente do movimento na horizontal.

Pensa assim, se no mesmo momento os dois fossem lançados verticalmente para cima e atingíssem a mesma altura antes de retornarem ao chão, eles teriam exatamente o mesmo tempo de vôo, né?

Então, no lançamento oblíquo a gente pode usar a mesma ideia e dizer que nesse caso os tempos de vôo são iguais, já que as alturas são iguais:

Ficamos com a alternativa (a).