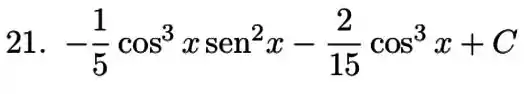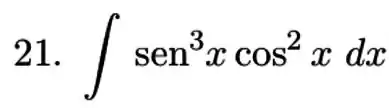
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 143123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos começar usando a identidade trigonométrica sen 2 ⁡ x = 1 - cos 2 ⁡ x

∫ sen 3 ⁡ x cos 2 ⁡ x d x = ∫ sen ⁡ x sen 2 ⁡ x cos 2 ⁡ x d x

∫ sen 3 ⁡ x cos 2 ⁡ x d x = ∫ sen ⁡ x cos 2 ⁡ x ( 1 - cos 2 ⁡ x ) d x

Passo 2

Vamos usar a técnica de substituição agora

u = cos ⁡ x

d u = - sen ⁡ x d x

Então nossa integral vai ficar

∫ sen 3 ⁡ x cos 2 ⁡ x d x = - ∫ u 2 ( 1 - u 2 ) d u

Manipulando um pouco

∫ sen 3 ⁡ x cos 2 ⁡ x d x = - ∫ u 2 - u 4   d u

∫ sen 3 ⁡ x cos 2 ⁡ x d x = - u 3 3 + u 5 5 + C

Desfazendo a nossa substituição

∫ sen 3 ⁡ x cos 2 ⁡ x d x = - cos 3 ⁡ x 3 + cos 5 ⁡ x 5 + C

Prontinho!

Passo 3

Maaas, se quisermos colocar a resposta igualzinho está na resposta da lista. Podemos fazer

cos 5 ⁡ x = cos 2 ⁡ x cos 3 ⁡ x

E substituir cos 2 ⁡ x = 1 - sen 2 ⁡ x

Então vamos ficar com

∫ sen 3 ⁡ x cos 2 ⁡ x d x = - cos 3 ⁡ x 3 + cos 3 ⁡ x 5 - sen 2 ⁡ x cos 3 ⁡ x 5 + C

∫ sen 3 ⁡ x cos 2 ⁡ x d x = - 2 cos 3 ⁡ x 15 - sen 2 ⁡ x cos 3 ⁡ x 5 + C

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x