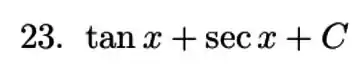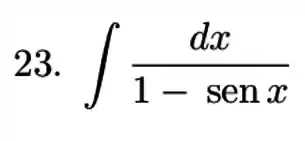
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Trigonométricas

Ver Teoria
Exercício 136123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Vamos começar? Primeiro precisamos determinar qual o conjugado no caso da nossa integral. Temos

∫ d x 1 - sen ⁡ x

O conjugado de 1 - sem ⁡ x é 1 + sem ⁡ x

Passo 2

Agora, como manda o enunciado do problema, vamos multiplicar a dividir a integral pelo conjugado.

1 1 - sen ⁡ x = 1 1 - sen ⁡ x ( 1 + sen ⁡ x ) ( 1 + sen ⁡ x )

=   ( 1 + sen ⁡ x ) 1 - sen 2 ⁡ x

Sabemos que cos 2 ⁡ x = 1 - sen 2 ⁡ x , então se substituirmos na expressão

1 1 - sen ⁡ x = 1 + sen ⁡ x cos 2 ⁡ x

= 1 cos 2 ⁡ x + sen ⁡ x cos 2 ⁡ x

= 1 cos 2 ⁡ x + sen ⁡ x cos ⁡ x   1 cos ⁡ x

= sec 2 ⁡ x + tan ⁡ x sec ⁡ x

Passo 3

Feitos esses ajustes, vamos aplicar isso na nossa integral

∫ d x 1 - sen ⁡ x = ∫ sec 2 ⁡ x d x + ∫ tan ⁡ x sec ⁡ x d x

E resolvendo as integrais

∫ sec 2 ⁡ x d x = tan ⁡ x

E

∫ tan ⁡ x sec ⁡ x d x = sec ⁡ x

Então

∫ d x 1 - sen ⁡ x = tan ⁡ x + sec ⁡ x + C

Prontinho, ficou bem mais fácil de resolver utilizando esse método né?

Resposta

Exercícios de Livros Relacionados

Deduza uma fórmula similar àquela do Exercício 41 para ∫ cot n ⁡ x d x ,s en for um inteiro positivo maior do que 1.
Calcule a integral. ∫ 0 π 4 sec ⁡ θ tan ⁡ θ d θ
Calcular a área da região limitada por y = tg^3 x , y = 1 e x = 0 .
Calcule a integral.int s e n^2 (pi x) cos^5 ( pi x ) d x
Calcule a integral.int s e n^6 (pi x) d x