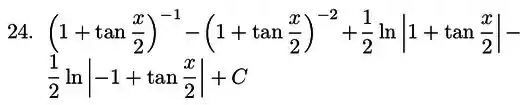Resolva a integral multiplicando e dividindo o integrando pelo conjugado.
Passo 1
Multiplicando pelo conjugado:
E como , a integral que temos que calcular é:
Passo 2
Essa integral da secante ao cubo é clássica, talvez você até já tenha se deparado com ela. A boa é fazer:
Ou seja:
Passo 3
Caímos em 2 integrais, então vamos por partes. No caso, literalmente, vamos integrar por partes hahaha. Pra calcular:
Fazemos
Assim:
Fazendo a integração por partes:
Passo 4
E a outra integral que temos é a da secante, que também é bem clássica. Lembra dela? Vimos na teoria:
Mas por enquanto não vamos nos preocupar com a constante, botamos ela no fim.
Passo 5
Enfim, juntando tudo:
Daí:
Ok, mas ainda não acabou!
Passo 6
Ainda falta a outra integral:
Fazendo a famosa substituição
temos:
Passo 7
Portanto, depois dessas contas todas, obtemos:
Resposta