3 - O gráfico abaixo representa o potencial elétrico em função da posição . Qual das alternativas descreve corretamente a componente do campo elétrico ao longo do eixo ?
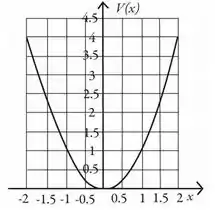
- é positiva de até
- é positiva de até e negativa de até
- é negativa de até e positiva de até
- é negativa de até
- é nula de até
Passo 1
Bem, sabemos que a tensão pode ser dada em relação ao campo elétrico através dessa integral de linha:
Como estamos falando do campo em função de produzido pela componente campo elétrico () ao longo do eixo , essa integral de linha vira uma integral mais simples:
Se você ficou curioso e quer saber por que veja o gráfico mostrando a componente do campo na direção de , bem como o também na direção de ( é o vetosinho que indica a linha que estamos medindo o potencial, no caso é o próprio eixo ):

Como e o vetor tem a mesma direção, o produto escalar dos dois é:
Como o trecho onde estamos medindo o potencial é o próprio , é simplesmente , saca?

Passo 2
Tá, beleza! Mas e aí? Bem, através desse gráfico...
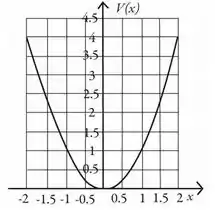
Podemos mais ou menos aferir que a tensão vale (ele tem o formato de uma parábola centrada no e ainda ) saca? Então...
Derivando de ambos os lados...
Isso significa que de até , o vai ser positivo e depois ele passa a ser negativo mesmo, saca? Então a resposta correta é a letra B.
Passo 3
Outra forma de verificar isso é que o campo elétrico sempre aumenta com a redução da tensão e vice versa!
Como de a a tensão é decrescente, o campo só pode ser crescente nesse trecho. De a é o inverso!
Resposta
Letra B.