Considere uma coroa circular com uma distribuição superficial de carga constante (estacionária e uniforme), onde . A coroa possui raio interno e raio externo e está localizada no plano , com o seu centro na origem, conforme ilustra a figura abaixo.
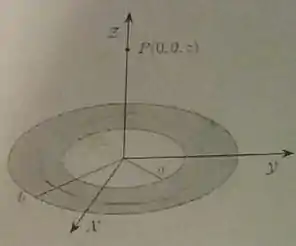
(a) Calcule o potencial eletroestático gerado por essa coroa circular no ponto , localizado no eixo , conforme ilustra a figura.
(b) Calcule o vetor campo elétrico gerado por essa coroa circular no ponto , localizado no eixo , conforme ilustra a figura.
Considere agora o limite em que o raio externo tende ao infinito, de forma que passamos a ter um plano infinito com um orifício circular de raio . A distribuição de carga contínua sendo uniforme, com densidade superficial . Para essa nova configuração, responda às perguntas a seguir.
(c) Considere que uma partícula de teste, de massa e carga , onde , tenha sido abandonada do repouso no ponto , Calcule a posição de equilíbrio da partícula no eixo . Adote a aceleração da gravidade como .
(d) Calcule a variação da energia potencial eletroestática da partícula de carga , a partir do momento em que ela foi abandonada do ponto , até passar pela origem do sistema de coordenadas.
Passo 1
O potencial elétrico causado por um infinitésimo de carga é dado por
Passo 2
Se tomarmos uma distância do centro do disco, temos uma carga ocupando uma área . A relação entre essas duas quantidades é dada por
Essa área em coordenadas cilíndricas é dada por
Assim, temos
Passo 3
Agora, voltando para o potencial
A distância é a distância entre a carga e o ponto . Pela figura podemos calcular usando teorema de Pitágoras.
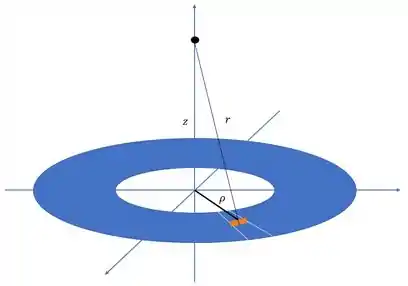
E o potencial fica
Agora basta integrar sobre o disco vazado
A integral radial fica moleza se fizermos a substituição
Assim
E a integral angular é simplesmente
Passo 4
É muito importante aqui enxergar como uma função de beleza? Porque o campo elétrico é igual a menos o gradiente de :
Afinal, só depende de e não varia com e . Derivando a gente pode encontrar o campo mais rápido do que fazendo uma integração de pequenos campos elétricos e começando tudo de novo.
Aí basta derivar em relação a .
Passo 5
Fazer tender ao infinito. Se isso acontecer o segundo termo do campo elétrico some:
Passo 6
Para que a carga fique em equilíbrio, a força gravitacional tem que ser igual ao campo vezes a carga:
Passo 7
Agora queremos a variação de energia potencial entre os dois pontos determinados na letra (d). Queremos o seguinte:
Que é a resposta da última letra da questão. Essa conta veio diretamente da definição de potencial elétrico :)
Resposta
(a)
(b)
(c)
(d)