Um anel circular de raio está carregado com uma densidade de carga positiva e não uniforme, , onde . Determine:
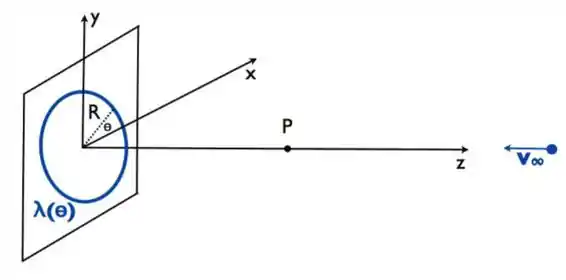
a carga total no anel.
o potencial eletrostático, , num ponto do eixo de simetria do anel, localizado a uma distância do seu centro (sabendo-se que no infinito).
a expressão do campo elétrico, , no ponto , a partir de .
o módulo da velocidade inicial, , que um próton, de massa e carga , deve ter, em , para que este chegue ao repouso no centro do anel, em
Passo 1
A carga total no anel será a soma de todos infinitésimos de carga do anel,
Sendo que a carga infinitesimal é dada por:
Porém a densidade de carga não é linear, o enunciado nos disse que ela é dada em função de por:
Assim,
Temos em função de duas variáveis , porém para integrarmos precisamos que ela fique em função apenas de . Assim vamos tentar escrever em função do ângulo .
Pela fórmula do comprimento de um arco, podemos escrever que
Passo 2
Bem, agora que temos em função do ângulo , podemos reescrever a equação de
Então podemos voltar a integral
Como e são constantes podemos colocá-los para fora da integral.
Como temos o módulo do seno, vamos separar a integral em duas a parte que o seno é positivo e a parte que o seno é negativa
Então dividimos em
Resolvendo as integrais ficamos com
Passo 3
Pela simetria do anel, teremos apenas na direção .
Como a carga Q já calculamos, temos que
Onde é a distancia do anel até o ponto , que por Pitágoras é dado por
Como é constante, pois o ponto é determinado
Assim, a integral de é
Passo 4
Agora, precisamos lembrar que o campo elétrico é igual a menos o gradiente do potencial elétrico .
Terminamos de descobrir a equação do potencial, então, basta fazer suas derivadas parciais, certo?
Como a expressão do potencial depende apenas da coordenada , então
Então,
Colocando as constantes para fora,
Fazendo a derivada chegamos em:
Passo 5
Vish!! Como que relacionaram velocidade com isso, não me lembro de nenhum fórmula que envolva velocidade?!
Calma meu cara Watson! Não tem mesmo nenhuma fórmula que envolva velocidade, então só nos resta pensar em energia cinética, certo?
Afinal, toda partícula em movimento possui energia cinética. E como não há forças externa a energia mecânica do sistema é conservada. Assim,
Podemos abrir isso, em energia potencial e energia cinética:
A energia potencial no infinito, temos que ela é adotada como zero, e a energia cinética em é zero, pois queremos que a partícula esteja em repouso.
Então, chegamos em
Passo 6
Primeiro vamos calcular a energia potencial em .
Temos que
Onde, vai ser a carga do próton ), e ainda, vamos substituir pela equação que encontramos no item
Substituindo por , temos que:
Passo 7
Podemos voltar a relação de energia cinética no infinito, agora
A fórmula de energia cinética, lembramos que é
A massa do próton foi dada, então temos tudo para calcular a velocidade no infinito do próton,
Como a partícula vem do infinito em direção ao centro, temos: