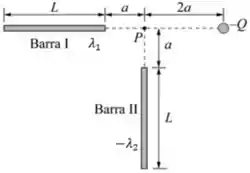
Q - A figura ao lado mostra duas barras isolantes de comprimento , que estão uniformemente carregadas com densidades lineares de cargas e , respectivamente, e uma carga puntiforme , situada a uma distância da Barra .
Determine o vetor campo elétrico, produzido no ponto , pelo conjunto (barras e carga).
Determine o potencial elétrico no ponto produzido pelo conjunto.
Supondo que , determine para que o campo elétrico faça um ângulo de com a horizontal.
Dica: Não se esqueça de explicitar qual é seu sistema de referências.
Passo 1
Vem comigo que a gente detona com essa questão!
Para achar o campo em temos que somar as contribuições dos da barra , da barra e da carga puntiforme nesse ponto. Para achar esses campos vamos usar a seguinte equação:
Para facilitar nossas contas vamos considerar a origem dos eixos coordenados no ponto . Onde o sentido positivo de é para a direita e o de é para cima.
Para achar o potencial elétrico pedido em , vamos usar a seguinte equação.
Onde nada mais é que a distância do elemento de carga até o ponto onde estamos querendo avaliar o potencial.
Para o item , temos que usar o fato que para o campo elétrico está a a sua componente tem que ser igual a sua componente pois
Logo:
Vamos calcular esses campos então!
Passo 2
Vamos começar com o campo produzido pela carga puntiforme. O campo dessa carga vai estar na direção que liga a carga e o ponto , então ele estará na direção .
Ela se encontra a uma do ponto , então a distância . Como estamos lidando com uma carga pontual, seu elemento de carga vai ser igual a carga da partícula, então temos que:
Mas como é um vetor que aponta da carga para o ponto onde queremos saber o campo, temos que esse na verdade é , com isso nosso campo é:
Esse campo então aponta para o sentido positivo do eixo .
Passo 3
Vamos agora calcular o campo que a barra faz em . O campo dessa barra no ponto vai estar na direção que liga a carga e o ponto , então ele estará na direção .
Para achar o campo da barra vai ser um pouco mais complicado já que ela não é um objeto pontual, então o campo elétrico gerado por ela em vai ser dado pela contribuição de cada pedacinho da barra.
A equação do passo dos dá o campo gerado por um elemento de carga em uma posição
.
O enunciado diz que a barra tem uma densidade linear de carga , isso quer dizer ela tem uma quantidade de carga por unidade de comprimento , então temos que:
Com isso temos o seguinte:
Esse é o campo gerado por um elemento de carga da barra a uma distância da origem, para achar da barra toda, vamos integrar os dois lados dessa equação, onde o lado esquerdo vai ser integrado de até , que da o comprimento da barra, assim temos:
Então temos que:
Passo 4
O raciocínio para calcular o campo da barra é igual ao da barra , só que a gora na direção , então temos o seguinte:
Então temos que:
Passo 5
Juntando tudo agora temos que o campo em , é dado por:
Passo 6
Vamos agora achar o potencial no ponto , para isso temos que achar o potencial que cada elemento do nosso sistema realiza em e depois soma-los.
Vamos começar com a carga , temos:
Só que como estamos lidando com uma carga pontual, não a necessidade de se resolver essa integral já que o elemento de carga está concentrado em um único ponto, assim:
Passo 7
Agora vamos encontrar o potencial da barra em , temos:
Como já vimos antes . E temos também que é igual a distância do elemento da barra até , então essa distância é .
E como queremos o potencial gerado por toda barra temos que considerar a contribuição de todos os da barra, então a integral fica de até , então:
Então temos que:
Passo 8
Para a barra o raciocínio é o mesmo que para a barra , só que agora temos , assim temos que:
Então temos que:
Passo 9
Agora vamos juntar tudo para acharmos o potencial total em , temos:
Passo 10
Agora vamos ver o que o item quer.
Ele fala para que agora consideremos , com isso o campo elétrico total fica da seguinte forma:
Dando uma ajeitada aí, cortando o termo que aparece no denominador e no numerador da fração, teremos:
Como já vimos no passo , para que esse campo esteja com um ângulo de com a horizontal, temos que:
Agora, isolando o , teremos:
Agora, vamos dar uma ajeitada nisso, colocando em evidência:
Pronto! Está tudo feito!