Potencial Elétrico, Campo Elétrico
Um bastão de comprimento , eletrizado com densidade de carga não uniforme está disposto ao longo do eixo .
Determine o potencial eletrostático devido ao bastão para um ponto sobre o eixo com coordenada . Adote o potencial nulo no infinito.
Determine o vetor força de interação eletrostática sobre uma carga pontual em .
Passo 1
Determine o potencial eletrostático devido ao bastão para um ponto sobre o eixo com coordenada . Adote o potencial nulo no infinito.
O primeiro passo aqui é escrever a expressão do potencial elétrico gerado por um pedaço infinitesimal do bastão, de carga .
Onde:
Obs.: Como o problema diz que o ponto está na posição , vamos chamar a coordenada acima de pra não nos confundirmos, beleza?
Onde . Assim, para determinar a expressão de , basta integrar a expressão de :
Antes de continuar com os cálculos, vamos analisar graficamente e pra não nos confundirmos aqui, ok?
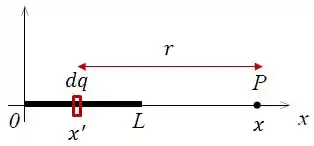
Daqui podemos tirar que:
Logo:
Pode ser que você se enrole um pouco pra resolver essa integral. Antes que isso ocorra, dê uma olhada no formulário da sua prova... em muitos casos, as respostas de integrais que vão cair na prova estão lá.
Finalmente:
Passo 2
Determine o vetor força de interação eletrostática sobre uma carga pontual em .
A força eletrostática sobre uma carga é dada por:
Então, a primeira coisa que temos que fazer é determinar o campo elétrico a partir do potencial que nós calculamos no item anterior.
O potencial e o campo elétrico estão relacionados por:
Como a carga está no ponto , basta jogar na equação acima pra encontrar a expressão do campo elétrico no ponto .
Finalmente, a força eletrostática sobre a carga será:
Resposta