Denomina-se coroa anular um disco fino de raio externo com buraco circular concêntrico de raio interno como mostrado em figura. Uma coroa anular possui uma densidade superficial de carga sobre sua superfície (.
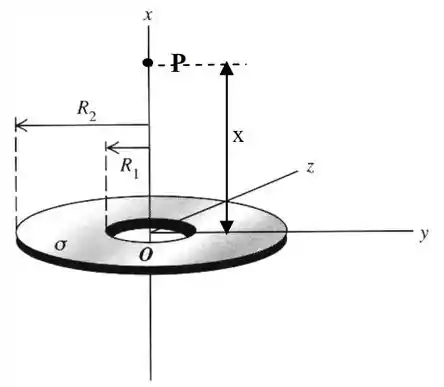
Determine a carga total sobre a coroa anular.
A coroa anular está sobre um plano com seu centro na origem. Para um ponto arbitrário sobre o eixo (eixo de simetria da coroa anular), determine o potencial (Sugestão: calcule o potencial devido a um anel de raio e espessura compreendido entre e e depois extenda o resultado para a coroa anular.)
Calcule agora o campo elétrico (módulo, direção e sentido) no ponto .
Uma carga positiva puntiforme é inicialmente colocada a repouso no ponto e a seguir liberada. Qual será a energia cinética desta carga quando passa no centro da coroa anular? (Considere neste item ; ; )
Passo 1
Para determinar a carga da coroa, basta lembrar da definição de densidade superficial:
Substituindo os valores, temos:
Onde , portanto,
Passo 2
Para calcular o potencial gerado pela coroa em qualquer ponto do eixo , devemos primeiro calcular o potencial geral por um anel de espessura infinitesimal, temos então:
Onde , substituindo:
Agora basta integrar de até :
Passo 3
Para determinar o campo elétrico, precisamos lembrar da seguinte relação:
Por simetria, vemos que o campo elétrico possui apenas componente , temos então:
Derivando, temos:
Passo 4
Para determinar a energia cinética, devemos utilizar a conservação da energia mecânica. No repouso, temos apenas a energia potencial elétrica, quando a carga passa pelo centro, teremos energia cinética e energia potencial elétrica, ou seja:
Lembrando que:
Agora, precisamos determinar a variação de potencial, considerando ; ;
Portando, a energia cinética ao passar no ponto , é:
Resposta