Considere uma esfera , de raio , uniformemente carregada com densidade volumétrica de carga positiva. Considere também três pontos no espaço, , e , onde os potenciais elétricos valem , e , respectivamente. Se está no interior da esfera, sobre sua superfície, e em seu exterior, temos, necessariamente,
Passo 1
Para matarmos essa questão, vamos considerar a superfície gaussiana esférica concêntrica à esfera e com raio , que está desenhada na figura abaixo.
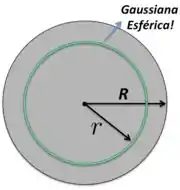
Como a esfera está uniformemente carregada com densidade de carga volumétrica positiva , isso significa que, dentro da gaussiana, teremos um carga de
Por outro lado, como temos simetria esférica, o campo elétrico produzido por , que está apontando para fora da gaussiana, é paralelo ao vetor infinitesimal de área em todos os pontos da superfície gaussiana. Além disso, o módulo desse campo depende apenas da distância ao centro e, por essa razão, tem o mesmo valor em todos os pontos da superfície gaussiana.
Colocando tudo isso dentro da lei de Gauss, teremos que
que vai dar um módulo do campo elétrico de igual a
Passo 2
Uma vez que temos , podemos calcular a diferença de potencial entre e através da expressão:
Como pode qualquer caminho ligando os pontos e , podemos escolher , que é paralelo ao vetor .
Com isso e substituindo que encontramos no Passo 1, vamos ter
Dessa expressão, tiramos que
já que para este caso.
Passo 3
Para , a carga total dentro da gaussiana esférica de raio é
enquanto que o lado esquerdo da lei de Gauss vai dar o mesmo resultado que encontramos no Passo 1: . Portanto, o campo elétrico será
Agora, como fizemos no caso do Passo 2, vamos tomar a diferença de potencial entre os potenciais e , que será
em que fizemos, como no Passo 2: . Com isso, vamos ter
Como estamos olhando para a região em que , a última expressão acima mostra
Com isso a gente fecha o problema e podemos comparar os potenciais da seguinte maneira:
Resposta
Letra f.