. Um plano infinito é posicionado sobre o plano de um sistema de coordenadas. Ele encontra-se carregado com uma densidade superficial de carga constante .
Sabendo que o campo elétrico produzido pelo plano em um ponto qualquer do espaço tem a forma , utilize a lei de Gauss para determinar , considerando as regiões e .
Determine o potencial elétrico produzido pelo plano no ponto , considerando as mesmas regiões acima. Considere que o potencial é nulo sobre o próprio plano.
Passo 1
Vamos lá então para mais esse problema e vamos acabar com ele!
O item pede que encontremos e que utilizemos a lei de Gauss, que nos diz que o fluxo do campo elétrico por uma superfície é igual a carga total no interior da superfície divido por , temos então que:
Só que para fazermos esse cálculo temos que definir uma superfície por onde teremos o fluxo do campo. Como o plano carregado é infinito temos que o campo embaixo do plano é igual ao campo encima em qualquer ponto, com isso vamos escolher a seguinte superfície:
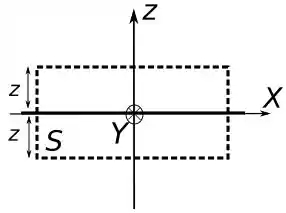
Onde o elemento de área aponta para fora da superfície em cada lado. Com isso poderemos desenvolver esse item e encontrar .
Agora para encontrar o potencial pedido em , vamos usar o fato de que
Onde essa integral não depende do caminho escolhido, mas sim dos pontos iniciais e finais.
Como enunciado já nos dá que o potencial no plano é nulo, vamos escolher como um ponto sobre o próprio plano e o ponto como o nosso ponto , com isso temos que:
Para continuar o problema precisaremos do campo que vamos encontrar em .
Vamos acabar com esse problema!
Passo 2
Então vamos lá, começando com o item , temos o seguinte:
Primeiro vamos lidar com o lado esquerdo e depois lidamos com o lado direito dessa equação.
Podemos separar essa integral em três integrais, que representa o fluxo pela parte superior e inferior da superfície e a parte a lateral, assim temos:
Agora vamos ver umas coisinhas, o enunciado nos diz que o campo só tem componente na direção , então na parte lateral teremos perpendicular a , logo , assim:
A integral nas superfícies superior e inferior são iguais, já que as superfícies são iguais, assim temos:
Passo 3
Usando o fato de que para um ponto qualquer temos:
E que como o elemento de área para a superfície superior aponta para a direção , temos:
Com isso nossa integral fica da seguinte forma:
Como é um vetor unitário, temos que e como a integral não depende de , temos que:
A integral de vai nos dá a própria área, assim temos que:
Passo 4
Agora vamos mexer com o lado direito da equação, que é:
Onde é a carga interna a superfície. O enunciado fala que a densidade superficial de carga é dada por e a superfície pega uma área do plano, temos que:
Juntando tudo temos o seguinte:
Agora pela simetria do plano temos que
Passo 5
Agora vamos mexer com item .
Do passo tínhamos que:
Como vimos no item o campo para um dado ponto nas regiões e , é dado por
E usando que já que o potencial em qualquer ponto do plano é zero segundo o enunciado, ficamos com:
Como eu disse no passo o caminho que tomamos pode ser qualquer um, com isso temos que:
Então temos o seguinte:
Temos que esse produto escalar entre e nos dá , logo só nos interessa a direção com isso temos que:
Passo 6
Para simplificar a nossa notação, vamos usar que para e para , teremos que:
Onde o valor do módulo muda dependendo da região que estamos olhando.