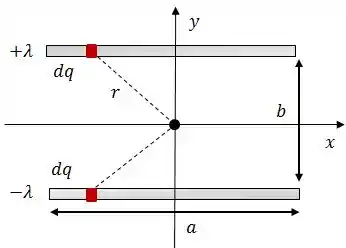
Dois fios retilíneos de mesmo comprimento , separados por uma distância , estão uniformemente carregados com densidades lineares de carga e .
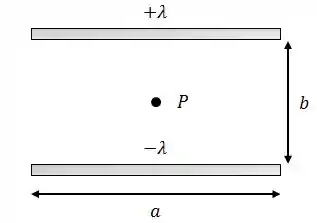
- Calcule o campo elétrico no ponto , centro do retângulo de lados e ;
- Calcule o potencial elétrico nesse ponto, supondo que no infinito;
- Se uma carga de prova for colocada no ponto , qual é a força instantânea que age sobre ela?
Passo 1
a) Calcule o campo elétrico no ponto , centro do retângulo de lados e ;
Beleza, nesse tipo de problema, o melhor caminho e fazer uma barra de cada vez, entender como vai ficar o campo elétrico para uma barra e estender o raciocínio para a outra.
Vambora!
Pra começar, nós vamos pegar uma parte infinitesimal do bastão, com carga e, a partir dela, chegar à expressão do campo elétrico da barra.
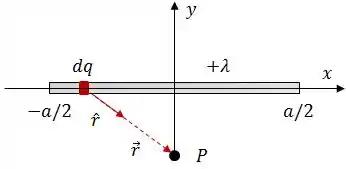
O campo elétrico gerado pelo elemento de carga é dado por:
Onde:
Logo:
Guarda isso que eu vou te falar agora, ok? Sempre que for resolver esse tipo de problema, você necessariamente vai ter que decompor o vetor de campo elétrico, beleza?
Então vamos fazer isso no próximo passo.
Passo 2
Olhando a figura, podemos escrever o vetor com . Consegue ver isso?
Isso acontece porque o vetor aponta no sentido negativo do eixo . Além disso, o vetor aponta no sentido negativo do eixo quando e no sentido positivo do eixo quando .
Continuando...
Sendo esse o vetor , a distância será:
Passo 3
Antes de voltarmos pra fórmula, repara que a carga infinitesimal pode ser escrita em função da densidade linear de carga .
O apareceu porque o bastão está posicionado ao longo do eixo .
Agora sim!
Passo 4
No passo 1, nós achamos o seguinte:
Nos passos 2 e 3, vimos que:
Substituindo tudo isso na fórmula, teremos:
Confere aí e vê se está tudo no lugar!
Antes de começar a esquentar a cabeça com toda a conta que vem pela frente, tem um jeito de simplificar isso aqui.
Se pegarmos dois pontos equidistantes e analisarmos o campo elétrico resultante, vamos ter o seguinte:
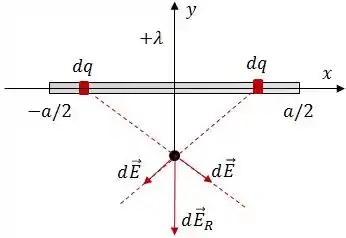
Como dá pra ver na imagem, as componentes na direção se cancelam, ou seja, se fossemos integrar a componente do nosso campo aí em cima íamos achar . Faz sentido né? Já que isso aí é uma função ímpar integrada entre e .
Isso significa que nós só teremos que nos preocupar com a componente na direção .
Passo 5
Voltando ao problema:
Acabamos de ver que podemos simplificar isso aqui para:
Agora é “só” integrar isso tudo!
Lembrando que varia entre e .
Bom, aqui não vale muito a pena ficarmos quebrando a cabeça com isso, então vou pelo menos te dizer como começar a resolver o problema, beleza?
A integral
é resolvida por substituição trigonométrica, se você chamar e .
Só vale lembrar que na prova você vai ter que quebrar a cabeça e resolver essa integral, então é mais fácil quebrar a cabeça agora e saber pra onde ir caso você tenha que resolver uma dessas na prova, beleza?
Resolvidas as integrais, você vai encontrar:
Quando nós substituirmos os valores, o primeiro termo já era, pode conferir, vai sobrar só o segundo termo:
Passo 6
Olhando agora pra barra com densidade linear de carga , dá pra ver que vai acontecer a mesma coisa que anteriormente, e o campo elétrico resultante vai continuar apontando pra baixo:
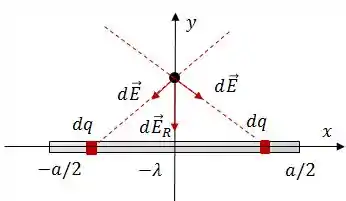
Então o campo elétrico resultante dessa barra vai ser exatamente igual ao da primeira barra. Logo:
Portanto, o campo elétrico resultante será:
Passo 7
b) Calcule o potencial elétrico nesse ponto, supondo que no infinito;
Vamos usar o mesmo princípio que usamos pro cálculo do campo elétrico. Vamos pegar um pedaço infinitesimal da barra com uma carga , escrever o potencial correspondente e a partir daí encontrar o potencial no ponto .
Sabendo que o potencial resultante é igual à soma do potencial, se pegarmos um ponto de cada barra com a mesma distância para o ponto , o potencial é dado por:
Lembrando que a barra superior possui um elemento de carga e a barra inferior possui um elemento de carga .
Logo:
Passo 8
c) Se uma carga de prova for colocada no ponto , qual é a força instantânea que age sobre ela?
Na letra nós vimos que o campo elétrico resultante é dado por:
Por definição, podemos associar o campo elétrico com a força elétrica por:
Logo:
Resposta
a.
b.
c.