Uma carga puntiforme está no centro de uma fina casca esférica condutora de raio , carregada com carga .
Justaposta a esta casca encontra-se uma camada de material dielétrico de constante dielétrica , tendo raio externo .
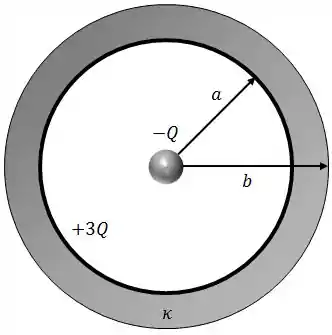
Encontra o vetor campo elétrico para , , ;
Calcule a ddp ;
Tomando , calcule para .
Passo 1
Encontra o vetor campo elétrico para , , ;
O campo elétrico é calculado através da lei de Gauss, dada por:
Para esse tipo de simetria, podemos simplificar a lei de Gauss e escrevê-la da seguinte forma:
Onde a gaussiana será uma esfera de raio , que engloba a carga .
Como o problema possui simetria esférica, o campo elétrico será radial, logo:
Então, o nosso trabalho agora é calcular a carga interna em cada região, beleza?
Passo 2
- :
- :
- :
- :
- :
- :
Essa região engloba somente a carga pontual , logo:
Essa região engloba a carga pontual e a casca esférica, logo:
Um detalhe que você tem que ficar esperto é que, como essa região está no interior do material dielétrico, ao invés de usarmos , usaremos , onde:
Substituindo esses caras na expressão de , teremos:
Essa região engloba todo o sistema, logo:
Sendo assim:
Passo 3
Calcule a ddp ;
Na letra nós vimos que, na região no interior do material dielétrico , o campo elétrico é dado por:
O campo elétrico e o potencial estão associados por:
Logo:
Passo 4
Tomando , calcule para .
Aqui o princípio é o mesmo da letra . Na região , vimos que o campo elétrico é dado por:
Assim, o potencial será dado por:
Resposta
Resposta
Ei, a resposta está no passo a passo :)