Um cilindro muito longo maciço condutor, de raio e densidade de carga por unidade de comprimento , é concêntrico a uma camada cilíndrica condutora carregada com a mesma carga total do cilindro, em módulo, e sinal oposto.
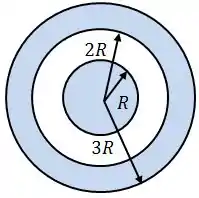
Essa camada tem raio interno e raio externo , como mostra a figura.
Determine o campo elétrico para as regiões e .
Determine a diferença de potencial entre os pontos e , ou seja, .
Passo 1
Determine o campo elétrico para as regiões e .
Para determinar o campo elétrico, vamos usar a Lei de Gauss, dada por:
Para isso, vamos selecionar uma gaussiana com a mesma simetria do corpo em questão, logo, com simetria cilíndrica.
Assim, usando com gaussiana um cilindro com um raio aleatório , teremos:
Onde corresponde ao comprimento do fio.
Assim, para cada região, basta determinar quanto vale a carga no interior da gaussiana.
Passo 2
- :
A gaussiana com o raio entre e engloba somente o fio com densidade de carga por unidade de comprimento , logo, utilizando a definição de densidade linear de carga, teremos:
Assim, substituindo na expressão que encontramos no Passo 1, teremos:
- :
Agora a gaussiana engloba tanto o cilindro, quanto a camada cilíndrica. Como o cilindro e a camada cilíndrica possuem cargas de mesmo módulo, mas com sinais opostos, a carga total no interior da gaussiana será:
Assim, o campo elétrico nessa região será:
Passo 3
(b) Determine a diferença de potencial entre os pontos e , ou seja, .
Show de bola! Para calcular os potenciais nesses pontos vamos usar a seguinte relação:
Como essa equação calcula uma diferença de potencial entre dois pontos, precisamos de um ponto de referência. Esse ponto de referência costuma ser o infinito, onde .
- :
Nessa região, o campo elétrico é nulo, logo:
Opa! Podemos agora calcular o potencial para .
Ok, vamos continuar analisando cada região do espaço, sempre “em direção ao centro do fio”.
Passo 4
- :
Essa região corresponde ao interior da camada cilíndrica condutora, e o campo elétrico no interior de um condutor é sempre nulo.
Além disso, agora vamos usar como ponto de referência o ponto , já que acabamos de calcular o potencial .
Logo:
Agora podemos calcular o potencial para , logo:
Passo 5
- :
Agora o campo elétrico varia com de acordo com a equação que encontramos no Passo 2:
Assim, para essa região, teremos:
Para , temos que:
Passo 6
- :
Essa região corresponde ao interior do fio cilíndrico condutor. Opa! Como esse fio também é condutor, o campo elétrico no seu interior será nulo. Logo:
Finalmente, o potencial para será:
Passo 7
Agora podemos finalmente calcular a diferença que o problema nos pediu!
Resposta
a)
-:
- :
b)