Dois anéis circulares, de mesmo raio , perpendiculares ao eixo , tem seus centros em e . Ambos possuem a mesma carga total , uniformemente distribuída.
- Determine o potencial elétrico devido aos anéis, em um ponto genérico do eixo , com abscissa , tomando tal potencial como zero no infinito ().
- Usando o potencial do item (a), determine o campo elétrico devido aos anéis, no mesmo ponto supracitado.
- Considere agora uma partícula de carga , ainda no mesmo ponto supracitado. Determine a energia potencial associada à interação dessa partícula com o campo elétrico produzido pelos anéis!
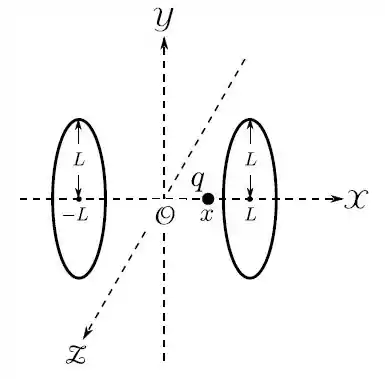
Passo 1
Como estamos tratando de anéis, a boa aqui é integral do potencial infinitesimal:
A expressão para ele nós temos da carga pontual:
Vamos fazer integrais separadas para cada anel. Para o de centro em temos:
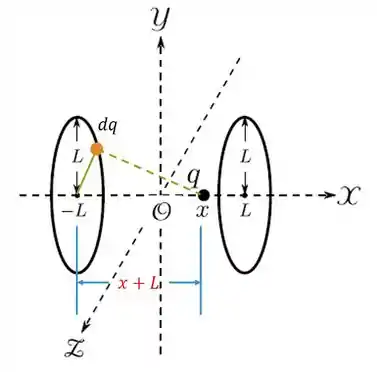
Passo 2
Como o triângulo verde é retângulo no vértice em que está , jogamos o Pitágoras:
Note como a distância é a mesma para todos os pontos do anel. Isso facilita a integral demaaaaais:
Se você se sentir mais confortável mostrando isso matematicamente, fique à vontade. Basta mostrar que o não está em função de .
Passo 3
Integrando infinitesimais em todo o anel obtemos a carga total deste:
Pela mesma lógica fazemos para o anel de centro em . Neste caso temos:
O potencial total é só a soma dos potenciais:
Fim de papo.
Passo 4
Dado que temos o potencial, achar o campo é moleza!!! Basta usar a fórmula do bem:
Onde o triangulo de cabeça pra baixo é o nosso operador de derivadas parciais:
Fazendo isso para o potencial, temos:
Passo 5
Já as outras derivadas, graças à Deus, dão zero pois o potencial não depende de nem de :
Logo:
Passo 6
Temos que a definição de potencial elétrico é a de energia potencial por unidade de carga, portanto:
Se quisermos a energia potencial basta multiplicar pela carga o potencial:
Morreu? = ]
Resposta
a)
b)
c)