A figura abaixo ilustra um anel fino não condutor de raio , com carga positiva uniformemente distribuída ao longo de sua circunferência.
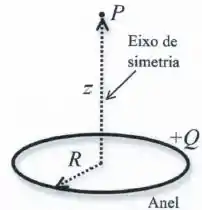
Considerando que o potencial elétrico é zero no infinito, calcule em um ponto que está localizado sobre o eixo de simetria do anel, a uma distância do seu centro.
A partir da expressão do potencial obtida em , calcule o valor da componente do campo elétrico na direção .
A expressão para obtida em permite calcular a componente do campo elétrico, mas não as componentes e . Por quê?
Uma partícula com carga elétrica e massa é lançada do infinito em direção ao anel, ao longo do seu eixo de simetria. Calcule a velocidade de lançamento mínima para que a partícula atravesse o plano do anel.
Passo 1
Considerando que o potencial elétrico é zero no infinito, calcule em um ponto que está localizado sobre o eixo de simetria do anel, a uma distância do seu centro.
Vamos começar com o potencial elétrico gerado por um pedaço infinitesimal do anel, com carga , dado por:
A distância de qualquer ponto do anel ao ponto é dada por:
Assim, substituindo na expressão de , teremos:
Agora basta integrar a expressão acima:
Onde a integral de será igual a carga do anel, logo:
Passo 2
A partir da expressão do potencial obtida em , calcule o valor da componente do campo elétrico na direção .
A componente do campo elétrico na direção é dada por:
Finalmente:
Passo 3
A expressão para obtida em permite calcular a componente do campo elétrico, mas não as componentes e . Por quê?
As componentes e do campo elétrico são dadas, respectivamente, por:
No entanto, de acordo com a expressão do potencial elétrico que encontramos no item , o mesmo depende somente de sobre o eixo de simetria do anel. Dessa forma, não podemos calcular as componentes e do campo elétrico pois o potencial elétrico independe dessas variáveis.
Passo 4
Uma partícula com carga elétrica e massa é lançada do infinito em direção ao anel, ao longo do seu eixo de simetria. Calcule a velocidade de lançamento mínima para que a partícula atravesse o plano do anel.
A energia mecânica do sistema é dada pela soma das energias potencial e cinética:
A energia potencial elétrica da partícula é dada por:
Substituindo a expressão que encontramos na letra , teremos:
Enquanto a energia cinética é dada por:
Quando a partícula está no infinito, a energia potencial é nula, só havendo a energia cinética. Para que a partícula atravesse o plano do anel, é necessário que, ao chegar no plano do anel , a energia cinética se anule, só havendo energia potencial.
No plano do anel, a energia potencial é dada por:
Assim, fazendo o balanço de energia nesses dois casos (partícula no infinito e no plano do anel), teremos:
Organizando os termos, vamos encontrar o seguinte:
Resposta