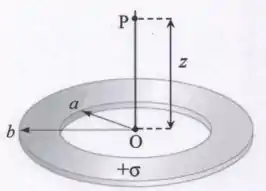
A figura abaixo ilustra um disco circular não-condutor oco, de raio interno , raio externo e centro , que tem uma densidade superficial de carga constante . O ponto está localizado a uma distância do ponto e o segmento define o eixo de simetria que passa pelo centro do disco oco, sendo perpendicular ao plano do disco. Considere que o potencial elétrico é zero no infinito, ou seja, . Nesta situação, calcule:
- O potencial elétrico no ponto .
- O vetor campo elétrico (módulo, direção e sentido) no ponto .
- A energia potencial elétrica adquirida por uma carga pontual que seja colocada no ponto .
Passo 1
a) Para calcularmos o potencial no ponto , temos que dividir o anel em várias faixas, cada uma com área infinitesimal , de raio () e com carga infinitesimal , cada uma distante de do ponto .
Para encontrar o potencial total devido à carga , temos que somar o potencial produzido por os elementos de carga que estão espalhados sobre toda a área do anel, lembrando que precisamos escrever o elemento de área como . Isso significa que o potencial no ponto será obtido a partir da seguinte integral
ou, ainda, como é constante em todo o anel, podemos simplificar a expressão acima para
Aqui, para resolvermos essa integral, podemos utilizar a substituição simples () e teremos que:
Passo 2
b) Como acabamos de ver das contas que fizemos, o potencial gerado por no ponto é uma função apenas da variável . Portanto, como sabemos que o campo eletrostático é dado por
ou seja, é igual a menos o gradiente do potencial eletrostático, e o potencial é uma função só de , o campo elétrico na direção vai ser obtido fazendo a seguinte conta:
que aponta na direção e sentido de , já que a carga do anel é positiva, dada por , e .
Passo 3
c) A energia potencial elétrica de uma carga negativa colocada no ponto será
em que é o potencial gerado por na posição . Portanto, substituindo na expressão que encontramos para o potencial no Passo 1, teremos que