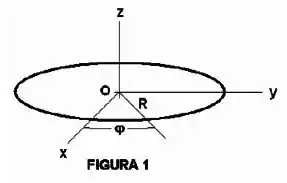
O anel de raio mostrado na Figura 1 tem a densidade linear de carga:
Determine uma expressão para o potencial elétrico em um ponto arbitrário do eixo (perpendicular ao plano do anel que contém a origem ).
é possível obter uma expressão para o vetor campo elétrico a partir do resultado do item ? Justifique sua resposta e determine as expressões para as componentes do campo elétrico para as quais a operação proposta seja possível.
Passo 1
Para determinar o potencial a uma distancia qualquer da origem, vamos começar com o potencial produzido por uma carga infinitesimal:
Onde , e é a distância entre cada carga e o ponto logo . Substituindo:
Integrando:
Passo 2
Podemos determinar o campo elétrico através da seguinte relação:
Como calculamos o potencial variando a distância , só poderemos determinar o campo nessa direção:
Resposta