Considere um fio retilíneo de comprimento , com densidadade linear de carga , posicionado conforme mostra a figura.
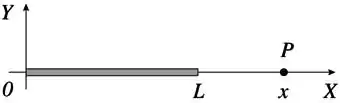
(a) Calcule o potencial elétrico em um ponto sobre a parte positiva do eixo de coordenadas , com . Assuma o potencial nulo no infinito.
(b) Calcule a componente do campo elétrico no ponto .
(b) Qual é o trabalho de uma força externa para trazer uma carga de prova do infinito até o ponto ?
Passo 1
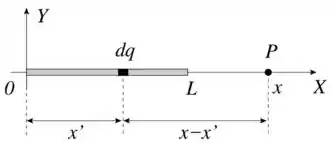
Para achar o potencial elétrico gerado pela barra temos que olhar para um elemento infinitésimo de carga que a constitui.
Supondo que este elemento esteja em uma posição ( o potencial gerado por esse elemento de carga será
Como a densidade linear de carga é , temos que
Assim
Passo 2
Agora temos que levar em conta todas as contribuições dos infinitésimos de carga
Passo 3
Temos que a componente do campo elétrico é dada por
Passo 4
Temos que o trabalho da força elétrica ao trazermos uma carga do infinito até o ponto se relaciona com a variação de energia potencial por
Já a energia interna se relaciona com o potencial elétrico por
Como , temos que
Mas o enunciado pede o trabalho de uma força externa! Nesse caso o trabalho da força externa será menos o trabalho da força elétrica.
Nesse caso