Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Potencial Elétrico Gerado por Corpos Extensos

Ver Teoria
Exercício 133123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

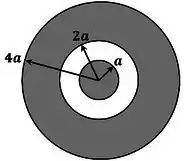
Uma esfera condutora de raio a , em equilíbrio eletrostático, possui carga - Q . Uma casca esférica espessa, condutora, de raio interno 2 a e raio externo 4 a , concêntrica à esfera, possui carga 2 Q , como mostra a figura abaixo. Considerando o potencial elétrico nulo no infinito, a que distância finita do centro da esfera o potencial também é nulo?

(a) 3 a / 2

(b) 4 a / 3

(c) 5 a / 4

(d) 6 a / 5

(e) 7 a / 6

(f) Não há nenhuma posição, a uma distância finita do centro da esfera, em que o potencial seja nulo.

Passo 1

Primeiro temos que ver como fica a distribuição de carga nessas esferas condutoras!

A primeira esfera tem carga - Q que irá ficar distribuída na sua superfície ( r = a )

Já na segunda esfera, para que o campo em seu interior seja nulo é necessário que uma carga + Q esteja distribuída em sua casca interna ( r = 2 a ) blindando o campo produzido pela esfera menor.

Como a esfera maior tem carga total 2 Q , sobrou uma carga Q para ser distribuída na casca externa da esfera maior!

Assim, resumindo, temos a seguinte distribuição de cargas:

- - Q , distribuída na esfera de raio a

- Q distribuída na cavidade interna de raio 2 a

- Q distribuída na esfera de raio 4 a

Passo 2

Agora já podemos usar a lei de Gauss, obter o campo elétrico e depois o potencial elétrico.

Vamos começar de fora pra dentro!

Com uma gaussiana que é uma esfera de raio r ( r > 4 a ), temos pela lei de Gauss

∫ E → d A → = q d e n t r o ϵ 0

A carga total dentro dessa gaussiana é q d e n t r o = 2 Q - Q = Q

Assim

∫ E → d A → = q d e n t r o ϵ 0 → E 4 π r 2 = Q ϵ 0

E → = Q 4 π ϵ 0 r 2 r ^

Assim a diferença de potencial, tomando como nulo o potencial no infinito

V r - V ∞ = - ∫ ∞ r E → . d r → = - Q 4 π ϵ 0 ∫ ∞ r 1 r ' 2

V r = Q 4 π ϵ 0 r ,   r ≥ 4 a

E esse potencial é sempre maior que zero na região r ≥ 4 a .

Passo 3

Temos que na região dentro do condutor externo que o potencial tem que ser constante. Como o potencial também tem que ser contínuo temos que

V r = Q 4 π ϵ 0 ( 4 a ) ,   ( 4 a > r ≥ 2 a )

E esse potencial é sempre maior que zero na região 4 a > r ≥ 2 a .

Passo 4

Agora na região entre os condutores ( 2 a ≥ r > a ), podemos de novo calcular o campo elétrico pela lei de Gauss. A diferença agora é que q d e n t r o = - Q (carga da esfera condutora menor).

O campo elétrico é dado por

E → = - Q 4 π ϵ 0 r 2 r ^

Assim agora tomemos 2 a ≥ r > a .

Cuidado com o sinal aqui, hein!!!

V r - V 2 a = - ∫ 2 a r E → . d r → = - ∫ 2 a r - Q 4 π ϵ 0 r 2 d r = Q 4 π ϵ 0 ∫ 2 a r d r r 2

V r - V 2 a = - Q 4 π ϵ 0 1 r ' 2 a r = Q 4 π ϵ 0 1 2 a - 1 r

Temos que o potencial em r = 2 a ( V ( 2 a ) ) é o potencial da casca esférica maior que já calculamos

V 2 a = Q 4 π ϵ 0 4 a

Assim

V r - Q 4 π ϵ 0 4 a = Q 4 π ϵ 0 1 2 a - 1 r → V r = Q 4 π ϵ 0 1 2 a + 1 4 a - 1 r

V r = Q 4 π ϵ 0 3 4 a - 1 r ,   2 a ≥ r > a

E esse potencial pode ser nulo! É só fazer

V r = Q 4 π ϵ 0 3 4 a - 1 r = 0 → 3 4 a - 1 r = 0

r = 4 a 3

E é nessa posição em que o potencial volta a ser nulo. Para distâncias menores que essa, o potencial fica negativo.

Resposta

(b)

Exercícios de Livros Relacionados

Uma barra de plástico tem a forma de um circunferência de raio R = 8,20 cm. A barra possui uma carga Q 1 = +4,20 pC uniformemente distribuída ao longo de um quarto de circunferência e uma carga Q 2 =
A Fig. abaixo mostra uma barra fina de plástico que coincide com o eixo x. A barra tem um comprimento L = 12,0 cm e uma carga positiva uniforme Q = 56,1 fC uniformemente distribuída. Com V= 0 no infin
O rosto sorridente da Fig. Abaixo é formado por três elementos: 1: Uma barra fina com uma carga de -3,0μ C e a forma de uma circunferência completa com 6,0c m de raio; 2: Uma segunda barra fina com um
Qual é o módulo do campo elétrico no ponto 3,00 i ^ - 2,00 j ^ + 4,00 k ^ m se o potencial elétrico é dado por V = 2 x y z 2 , em que V está em volts e x, y e z estão em metros?
Um elétron é colocado no plano xy, onde o potencial elétrico varia com x e y de acordo com os gráficos da figura abaixo (o potencial não depende de z) . Em termos dos vetores unitários, qual é a força