Questão discursiva – UFCG – Calculo diferencial e integral I – Lista 9 – teste – Lista UAMat – Lista 2 – derivadas – questão 14 item f
Derive:
f)
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
A questão nos pede para calcularmos a derivada de uma tal função. Como fazer isso? Bom, que tal vermos a definição. Mas antes, o que é a derivada?
Imagine que temos:
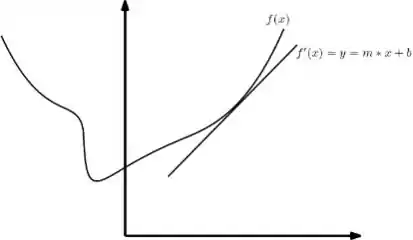
Imagine que temos uma função qualquer e temos então sua reta tangente num ponto qualquer. Mas essa reta tangente realmente toca num só ponto? Podemos provar isso? Por exemplo ela toca em mas não em ? Podemos dizer que não, certo? Então uma visão de perto da reta no ponto:
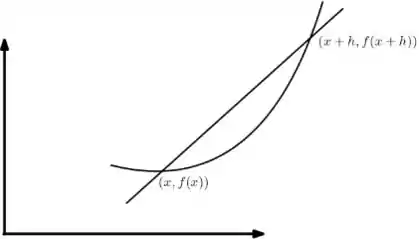
Onde é um passo instantemente depois.
Da reta tangente, sabemos que:
Ou o famoso “ioiô-m-xoxo” que tanto aprendemos. Assim:
Que é:
Mas como garantiremos que qualquer derivada seja exatamente num ponto? Teremos que fazer que o passo seja muito pequeno. Logo vamos tomá-lo indo para , ou seja, tendendo a . Assim:
E este é, portanto, a definição de derivada!! Portanto se queremos saber a derivada da função num ponto, basta aplicarmos essa definição de derivada da função no ponto e analisarmos seus limites.
Então vamos lá?!
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Temos então:
Temos dado que , logo . Portanto:
Sabemos que o seno da soma é dado por . Assim:
Também sabemos das propriedades das potencias que De forma que:
Sabendo que o limite da soma é a soma dos limites, podemos fazer:
E então podemos analisar cada limite separadamente para acharmos a derivada de
Passo 3
Para o primeiro:
Vemos que se fizemos temos uma indeterminação:
Então podemos aplicar uma sacada genial dos limites: A regra de l’hospital!! Ele é usado quando termos indeterminações num limite. Então derivando em cima e embaixo:
Sabendo que a derivada de em relação à é , temos que que é e da mesma forma . Mas veja que temos o produto de duas funções que dependem da variável que estamos derivando, de forma que temos que aplicar a regra do produto. Lembra dela?
De forma que:
Mas podemos fatorar essa coisinha, né?! Então fatorando , temos que fica:
Então concluímos que:
MAS, PALMA... palma, palma, não priemos cânico. Lembra do cosseno da soma? A saber, ele é , então vemos que:
Assim fica mais bonito nosso limite, veja:
Agora sim, veja que se fizermos , ou seja, no ponto, temos:
E achamos o resultado do nosso primeiro limite. Vamos para o segundo?
MAS ANTES... Você pode estar se perguntando: “Por que essa regra de l’hospital é verdade?” Porque temos um teorema poderoso da continuidade que nos diz que se uma função existe num ponto, sua derivada também existe nesse ponto. Aliás, isso que fizemos na demonstração do passo 1 quando falamos da definição de limite. E se no ponto é indeterminado, se a derivada no ponto existir então a função existe no ponto. Sacou?
Passo 4
Para o segundo:
Novamente, veja que se fizermos dará uma indeterminação
E quando temos uma indeterminação significa que novamente podemos usar a regra de l’hospital
Então derivando:
Mas veja que não depende de , logo ele é constante para , certo? Então a derivada de algo constante, como sabemos, é nula. Assim:
E, portanto:
E achamos o valor do nosso segundo limite.
Agora vamos descobrir como é a nossa derivada?
Passo 5
Então tínhamos:
E descobrimos que:
Logo concluímos que:
E achamos, portanto, a derivada de
E terminamos por aqui. Camarada. Obrigado por ter vindo até aqui comigo. Até a próxima!