Um cabo coaxial é composto por um fio sólido, cilíndrico, circular, de raio , envolto por uma casca espessa, cilíndrica, também circular, coaxial, de raios e , tais que . Ambos os cilindros são muito longos e tem o eixo comum . Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de corrente é dada por , onde e é a distância até o eixo do fio. Através da casca externa, passa uma corrente estacionária, cuja densidade de corrente é dada por , onde .

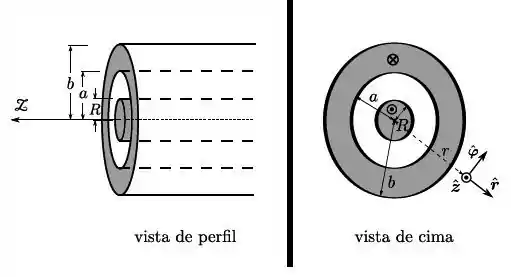
1. Qual é a (intensidade de) corrente elétrica no fio interno?
2. Qual é a (intensidade de) corrente elétrica na casca externa?
3. Determine o campo magnético em cada uma das quatro regiões em que o cabo “divide” o espaço.

Mesma coisa para a casca:

Que é a área da coroa circular de raios e :

Vamos fazer um argumento genérico para o espaço todo e depois ir achando as correntes. Enunciando a Lei de Ampère:

Pela configuração do campo magnético (i.e. do fio retilíneo longo), é ideal escolher uma curva Amperiana circular de raio arbitrário . De forma que:

Em toda , o que implica:

Além disso temos que, pela configuração do campo, o módulo deste é constante em toda , portanto:

A integral de pedaços infinitesimais na Amperiana resulta no comprimento desta:

Como se trata de uma circunferência de raio , temos:

Além disso, pela configuração do campo multiplicamos por para obter o vetor campo:

Agora vamos calculando as correntes de cada região. Para :

Substituindo:

Para temos que a corrente é igual à corrente total do fio interno:

Substituindo:

Na região temos que a corrente interna é tanto do fio quanto da parte da casca que está dentro da Amperiana. Portanto:

A primeira nós já sabemos, logo:

Agora vamos descobrir a corrente da casca:

A área da parte da casca dentro da Amperiana de raio é a coroa circular de raios e :

Logo:

Substituindo:

Por fim, para a região a corrente interna é a soma das correntes:

Portanto o campo fica: