Um fio extremamente longo é dobrado na forma mostrada na figura, de forma a evitar o contato no ponto de cruzamento . O raio da parte circular é e a corrente tem o sentido indicado.
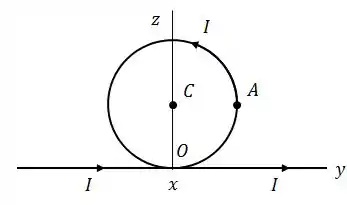
Determine a contribuição da parte linear do fio para o vetor campo magnético no centro e no ponto do círculo.
Determine a contribuição da parte circular do fio para o vetor campo magnético no centro do círculo e o vetor campo magnético total no mesmo ponto.
Em seguida, a parte circular do fio é girada de , sem distorção, em torno do eixo , tornando-se perpendicular à parte linear, de tal forma que a nova posição do ponto tem coordenada positiva.
Determine uma expressão para o vetor campo magnético total no centro do círculo.
Passo 1
Determine a contribuição da parte linear do fio para o vetor campo magnético no centro e no ponto do círculo.
Ambos os ponto e estão à mesma distância do fio retilíneo, isso significa que os campo magnéticos nos dois pontos, gerado pelo fio retilíneo serão iguais.
O campo é calculado a partir da lei de Ampère, dada por:
Devido à geometria do problema, a amperiana será uma circunferência de raio que engloba o fio retilíneo de corrente , logo:
De acordo com a regra da mão direita, nos pontos e , o campo magnético estará no sentido do vetor , logo:
Passo 2
Determine a contribuição da parte circular do fio para o vetor campo magnético no centro do círculo e o vetor campo magnético total no mesmo ponto.
O campo magnético gerado pela parte circular no ponto será calculado pela lei de Biot-Savart, dada por:
Onde é o vetor cujo módulo corresponde a um pedaço infinitesimal do fio e está sempre na mesma direção e sentido da corrente e é o vetor unitário que sai de um ponto no condutor e aponta para o ponto onde estamos calculando o campo magnético.
Vamos analisar esse cara graficamente:
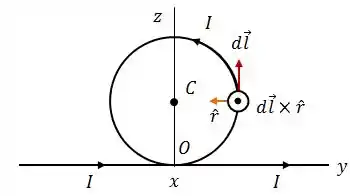
Daqui podemos concluir que:
Logo:
Passo 3
O campo magnético resultando no ponto será:
Passo 4
Determine uma expressão para o vetor campo magnético total no centro do círculo.
Ao girarmos a parte circular, de tal forma que a nova posição do ponto passe a ter coordenada positiva, nós também “giramos” o campo magnético gerado pelo anel no ponto .
Assim, tendo em mente a nova posição da parte circular, o campo magnético por ela agora será:
Como não há mudança no parte linear, o campo magnético gerado por ela permanece a mesma.
Assim, o campo magnético total no ponto será:
Resposta