UFRJ- Física 3 – PF 2018.2 - DIURNO – 11
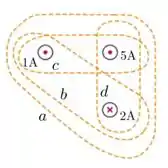
A figura abaixo mostra três fios condutores finos, retilíneos e infinitos transportando correntes estacionárias com as intensidades e sentidos indicados. Considere as quatro curvas fechadas , , e indicadas na figura. Seja o módulo da circulação do campo magnético resultante ao longo da curva (). Nesta situação, podemos afirmar que:
Passo 1
Pela lei de Ampère, a gente sabe que a integral de linha do campo magnético ao longo da curva fechada () é igual a:
em que é a corrente total que atravessa a área definida pela curva fechada . Como as curvas fechadas da figura do problema não estão orientadas, basta olharmos para a corrente total que atravessa cada uma das curvas.
Se elas têm sentidos contrários, então subtraímos uma da outra e jogamos do lado direito da equação acima; se elas têm mesmo sentido, então as somamos.
Passo 2
Começando pela curva , a corrente total é
Curva :
Curva :
Curva d:
Por isso, temos a seguinte ordem para os módulos das circulações:
Resposta
Letra a).