Considere dois fios retilíneos, longos, paralelos, separados por uma distância , pelos quais passam correntes estacionárias e no mesmo sentido. É correto afirmar que o campo magnético resultante será nulo em uma reta coplanar com os fios paralelos aos mesmo que esteja localizada:
- A uma distância de cada um dos fios.
- A uma distância do fio com corrente e do fio com corrente
- A uma distância do fio com corrente e do fio com corrente
- A uma distância do fio com corrente e do fio com corrente
- O campo magnético resultante devido aos dois fios não será nulo em ponto algum.
Passo 1
Bom, a primeira coisa é desenhar a situação para conseguirmos compreender:
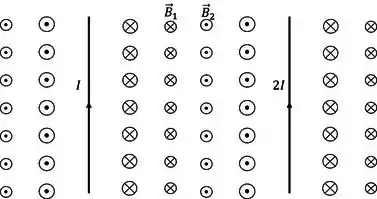
Agora sim. Podemos ver que o único jeito do campo dar zero em algum lugar é entre os dois fios, justo? Somente lá os campos tem sentidos opostos. Rodamos a Lei de Ampère bastante rápido para achar o campo:
Passo 2
Agora nós sabemos o módulo do campo à uma distância de um fio qualquer. Fazendo a soma dos campos num ponto dar zero:
Substituindo os valores:
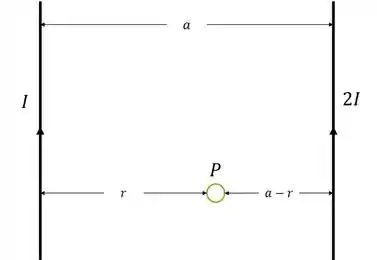
Passo 3
Resolvendo, corta-corta nas constantes:
Onde é a distância do ponto até o fio de corrente . Portanto ele dista do fio de corrente .
Resposta
Letra b