UFPE – Física 3 – 2019.2 – 3° EE – Discursiva
. A densidade de corrente no interior de um fio cilíndrico muito longo e retilíneo de raio é paralela ao eixo do cilindro. Seu módulo varia linearmente com a distância radial de acordo com a equação , onde é uma constante.
Calcule o campo magnético para .
Calcule o campo magnético para .
Passo 1
Vem comigo e vamos resolver esse problema!
Para esse problema vamos usar a lei de Àmpere, dada por:
Mas para achar o campo fora do fio pedido em e o campo dentro do fio pedido em precisamos traçar uma curva nessas regiões para cada caso.
E teremos também que calcular a corrente interna cada circunferência, já que temos uma densidade de corrente. Vamos calculá-la da seguinte forma:
Que em coordenadas cilíndricas, temos:
Onde vai depender de onde vamos traçar a circunferência , para uma circunferência com raio maior que o cilindro teremos e para uma com raio menor teremos .
Passo 2
Vamos começar com o item . Para ele vamos traçar a seguinte curva:
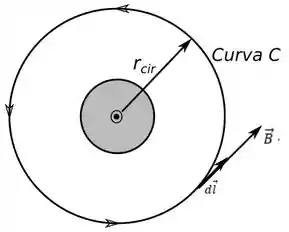
Como podemos ver o campo tem a mesma direção que logo temos que:
Essa integral sobre na curva nos dá o comprimento do círculo, assim:
Agora temos que achar .
Passo 3
Vamos lá então, temos:
Logo temos que:
Com isso o campo para é dado por:
Passo 4
Agora vamos encontrar o campo para a região do item . Temos a seguinte curva:
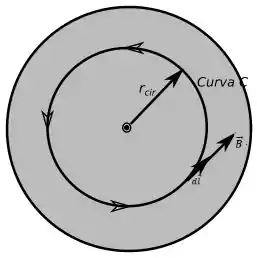
Como podemos ver o campo tem a mesma direção que logo temos que:
Essa integral sobre na curva nos dá o comprimento do círculo, assim:
Agora temos que achar .
Passo 5
Vamos lá então, temos:
Logo temos que:
Com isso o campo para é dado por: