Um contorno amperiano planar engloba dois fios retilíneos por onde fluem as correntes e . Todos os sentidos estão indicados na figura a seguir. O fio corta perpendicularmente o plano que contém o contorno , mas o fio o faz segundo o ângulo ().

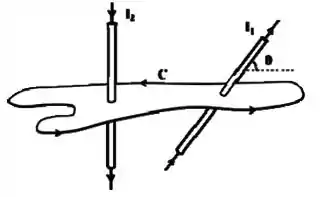
Sabendo que e que a integral ao longo de fornece o valor , encontre o valor da intensidade de corrente .

Sabendo que e que a integral ao longo de fornece o valor , encontre o valor da intensidade de corrente .

Opa! Quando o problema falou em integral , já temos que associar com a Lei de Ampère:

Beleza! A segunda coisa importante aqui é que você não deve se preocupar com esse ângulo que aparece, até porque a Lei de Ampére não diz nada em relação a isso... temos apenas que nos preocupar com as corrente que passam pela nossa amperiana, beleza?

Para saber quais correntes você considera positiva e quais você considera negativa, basta olhar o sentido da amperiana. De acordo com a regra da mão direita, vemos que o sentido da corrente é positivo para cima e negativo, para baixo.

Sendo assim:

Já que queremos descobrir o valor de , vamos substituir por .