Um cilindro condutor, maciço, de raio possui densidade de corrente estacionária e não uniforme dada por , onde é uma constante positiva, é a distância ao eixo do cilindro e é o unitário da direção correspondente a esse eixo.
- Determine a corrente total que atravessa uma seção transversal do cilindro.
- Determine o campo magnético (módulo, direção e sentido) produzido pelo cilindro em todo o espaço. Justifique cuidadosamente todos os argumentos utilizados.
Passo 1
a) Para calcularmos a corrente total que atravessa a seção transversal do cilindro, precisamos calcular a seguinte expressão
em que o vetor área é perpendicular à seção transversal, apontando na mesma direção e sentido do vetor , como mostra a Figura abaixo.
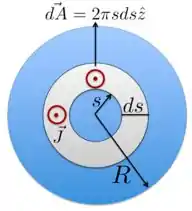
Temos, então, . Portanto, esse vetor é paralelo ao vetor densidade de corrente . Por isso, se substituímos essas informações juntamente com a expressão dada no enunciado, temos que a corrente é
Simplificando essa expressão, temos que a corrente total é
em que é o número de Euler.
Passo 2
b) Vamos calcular o campo magnético primeiro para :
Para isso, vamos considerar o cilindro desenhado na Figura abaixo, com a amperiana com sentido dado também na Figura.
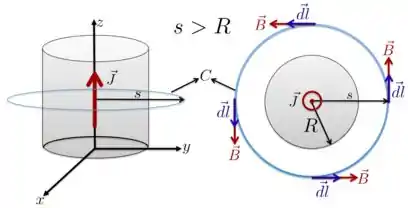
Como a corrente está ao longo do eixo , então o campo magnético vai estar na direção e, portanto, é paralelo à em todos os pontos da amperiana . Além disso, pela expressão para , vemos que o campo só depende da distância ao centro do cilindro. Por isso, o campo magnético produzido por essa corrente terá o mesmo valor em todos os pontos sobre a curva fechada (amperiana) .
A corrente total que passa através da área definida pela curva fechada já conhecemos e calculamos no item a): . Colocando isso tudo dentro da lei de Ampère, teremos
Para esse caso (), o campo magnético
em que é o número de Euler.
Passo 3
b) Agora para o caso em que
Para esse caso, considere a curva fechada (amperiana ) desenhada na Figura abaixo dentro do cilindro.
Novamente, o campo magnético estará ao longo da direção e sentido do vetor e terá o mesmo valor em todos os pontos sobre a curva .
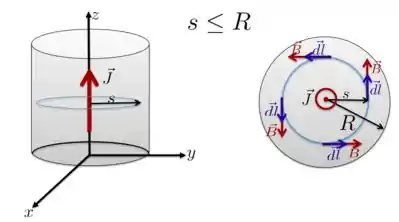
Agora, o que muda é que a corrente que atravessa a área definida por é diferente. Precisamos, então, encontrar qual é a corrente que passa atravessa da área circular de raio . Portanto, precisamos fazer a seguinte integral
Resolvendo essa integral, teremos que
Juntando esse valor para a corrente e as informações acima sobre o campo sobre a curva , obtemos, a partir da lei de Ampère, que
Simplificando essa expressão, temos que o vetor é dado por
Uma maneira de confirmar esse resultado, é colocar na expressão acima para tentar recuperar o campo magnético que obtivemos para ! ;-)
Resposta
- ;
- ;