1. Considere um fio condutor retilíneo, muito longo, percorrido por uma corrente elétrica estacionária de intensidade . Utilizando a Lei de Ampère e que o campo magnético provocado por tal fio retilíneo é puramente circular (ou azimutal), deduza, detalhadamente, uma expressão para tal campo, indicando, com clareza, qual a curva Amperiana utilizada (Sugestão: use coordenadas cilíndricas)
2. Utilizando a Lei de Biot-Savart, deduza, detalhadamente, o campo magnético , no centro de um anel condutor circular, de raio , percorrido por uma corrente elétrica estacionária de intensidade .
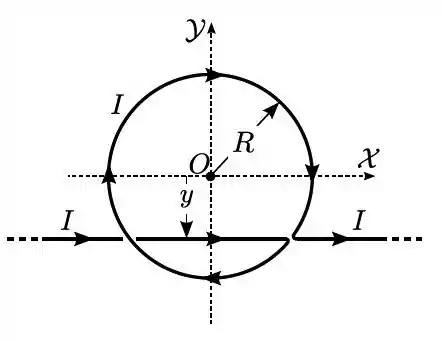
3. Referindo-se agora à figura abaixo, temos um arame com uma parte retilínea muito longa e outra parte circular, de raio e centro . Utilizando os resultados dos itens anteriores, qual deve ser a posição (ordenada) da parte retilínea do arame, de modo que o campo magnético resultante no ponto seja nulo?

Além disso temos que, pela configuração do campo, o módulo deste é constante em toda , portanto:

A integral de pedaços infinitesimais na Amperiana resulta no comprimento desta:

Como nossa Amperiana é uma circunferência de raio , temos que seu comprimento é:

Além disso, a corrente que atravessa a Amperiana é:

O campo fica em um sentido girando em torno do fio retilíneo. Podemos determinar o sentido pela regra da mão direita, se colocarmos nosso polegar no sentido da corrente, os outros dedos dão o sentido do giro. Estipulando que o vetor tenha este sentido de giro, temos que o campo fica:

Vamos agora rodar Biot-Savart para o campo do fio circular no centro. Enunciamos:

Sabemos que a corrente é constante e em nosso domínio de integração temos , portanto:

Para determinar o sentido do produto vetorial precisamos saber o sentido do eixo , portanto, pelo macete do prisma temos:

Agora sabendo que o eixo sai da tela, podemos achar o sentido do produto vetorial:

O comprimento do círculo de raio é conhecido:

Showz.

Queremos saber qual a distância do fio até o eixo para que dê campo nulo no centro. Vamos ser razoáveis e ignorar a sugestão da figura e supor tudo positivo. Vamos usar a regar da mão direita, com o polegar no sentido da corrente e os dedos acompanhando o campo Magnético. Lembra que o vetor não tem direção constante? Se o fio retilíneo estiver acima do eixo , o campo que ele produz vai entrar na página, ou seja, no sentido contrário de . Nesse ponto,

Além disto, a distância passa a ser . Ou seja:

Somando tudo e igualando a zero:

Agora é só resolver. Arrumando:

Isolando :

Ou seja, nossa suposição inicial de que a coordenada era positiva estava errada, mas a álgebra veio ao resgate e deu tudo certo no final. Na realidade o fio deve estar abaixo do eixo para que consigamos campo nulo no centro. Fim de papo.