Um resistor cilíndrico de raio é feito de um material de condutividade e permissividade dielétrica igual ao do vácuo. Uma voltagem variável é aplicada de tal modo que a corrente através do resistor é dada por no sentido do eixo , conforme a figura.
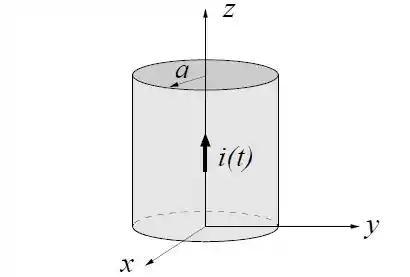
Determine o vetor densidade de corrente elétrica devido às cargas, supondo que seja uniforme no interior do resistor.
Determine o vetor campo elétrico usando a lei de Ohm.
Determine o vetor densidade de corrente de deslocamento .
Use a lei de Ampère- Maxwell para determinar o vetor campo magnético no interior do resistor a uma distância do seu eixo.
Passo 1
Determine o vetor densidade de corrente elétrica devido às cargas, supondo que seja uniforme no interior do resistor.
Como a corrente está se deslocando no sentido do vetor , a densidade de corrente, por definição será dada por:
Como a corrente independe da área, podemos dizer que:
Onde e . Portanto:
Passo 2
Determine o vetor campo elétrico usando a lei de Ohm.
O campo elétrico está associado à densidade de corrente por:
Eu sei que o problema não fala na resistividade , mas fala na condutividade . Os dois estão associados por:
Logo:
Substituindo a expressão de , teremos:
Passo 3
Determine o vetor densidade de corrente de deslocamento .
Por definição, a corrente de deslocamento é dada por:
Onde:
Como a área é constante, podemos dizer que , sendo assim:
Como a corrente independe da área, a densidade de corrente será dada por:
Logo:
Agora podemos começar a brincar! :D
Substituindo a expressão de que encontramos anteriormente, teremos:
Passo 4
Use a lei de Ampère- Maxwell para determinar o vetor campo magnético no interior do resistor a uma distância do seu eixo.
A lei de Ampère-Maxwell é dada por:
A nossa amperiana aqui é uma circunferência de raio , logo:
A corrente de condução é a corrente dada pelo problema, logo:
A corrente de deslocamento , por definição, é dada por:
Substituindo a expressão de , teremos:
Passo 5
Agora que já calculamos e , o campo magnético será dado por:
O campo magnético terá sempre direção tangencial, portanto:
Resposta