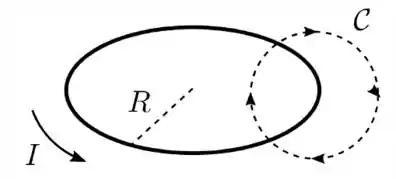
Uma espira condutora circular de raio transporta uma corrente estacionária de intensidade com sentido indicado na figura abaixo. Traça-se, então, uma curva amperiana circular , de raio , perpendicular ao plano da espira, com centro em um ponto da mesma e com a orientação indicada. Sobre essa situação, é CORRETO afirmar que:
- Pela lei de Ampère, o campo magnético produzido pela espira tem o mesmo módulo em todos os pontos de .
- Por simetria, o campo magnético produzido pela espira é tangente a em todos os pontos desta curva.
- Pela lei de Ampère, o campo magnético produzido pela espira é tangente a em todos os pontos desta curva.
- Por simetria, o campo magnético produzido pela espira tem o mesmo módulo em todos os pontos de .
- A circulação do campo magnético produzido pela espira ao longo de vale .
Passo 1
Vamos dar uma olhada para a lei de Ampère antes de começarmos a discutir os itens. Essa lei afirma pra gente o seguinte:
ou seja, a circulação do campo magnético é igual a vezes a corrente que atravessa a curva fechada .
Como os pontos da curva estão a distâncias diferentes dos pontos da espira de raio , o módulo campo magnético que gera sobre esses pontos tem valores diferentes e as direções e sentidos dos vetores também serão diferentes sobre os pontos da curva , como discutir melhor no próximo passo.
Passo 2
Basicamente, o problema está colocando afirmações sobre o módulo, direção e sentido do campo magnético produzido por sobre os pontos de . Por isso, pra gente matar essa questão, é importante voltarmos lá na lei de Biot-Savart, que diz o seguinte:
isto é, o campo magnético gerado por em um ponto a uma distância varia com e que a direção e sentido de são dadas pelo produto vetorial , sendo que é um vetor que tem a mesma direção e sentido da corrente em todos os pontos e é um vetor unitário que sempre aponta de para o ponto onde queremos calcular .
Vamos pegar a figura do problema e analisar só o elemento que indicamos na figura abaixo. Nesta figura, está a uma distância do centro de e está saindo do plano página, sendo perpendicular a ela. A corrente que passa por ele produz um campo infinitesimal , que está desenhado na figura para quatro pontos diferentes da curva fechada .
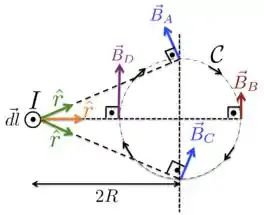
Como os pontos e da figura estão à mesma distância do elemento , os módulos dos campos e são iguais, porém suas direções e sentidos são diferentes, como mostra a figura acima. Além disso, os módulos dos campos são diferentes sobre os pontos da curva , sendo que os vetores são tangentes à apenas nos pontos e .
Com isso, todo os itens de a , estão INCORRETOS.
O item é exatamente o enunciado da lei de Ampère aplicado à curva , já que a única corrente que atravessa a área definida por é , dando para a circulação do campo magnético o valor de .
Resposta
Letra e.