Considere a função
(a) Determine e classifique os pontos críticos de em todo o .
(b) Determine os pontos de máximo e mínimo de sobre a circunferência:
(c) Determine os valores máximo e mínimo de no disco
e os pontos onde estes valores ocorrem.
Passo 1
(a)
Assim que a gente vir essas palavrinhas mágicas, “classifique os pontos críticos”, o nosso reflexo tem que ser: calcular as derivadas parciais, igualá-las a 0 e depois mandar ver no teste da derivada segunda! Então vamos fazer isso, começando pelas derivadas parciais:
Passo 2
Show! Agora vamos igualar essas derivadas a 0:
Ou seja:
Excelente! Isso nos dá os pontos críticos e .
Passo 3
Agora só resta classificar esses pontos críticos, usando o teste da derivada segunda, então vamos calcular as derivadas segundas! Lembrando que e , vamos ter:
E pras derivadas mistas:
Passo 4
Pronto! Agora podemos aplicar o teste da derivada segunda :) O nosso determinante vai ser:
E a gente tinha a achado os pontos críticos e , né? Nesses pontos vamos ter:
E . Logo, o ponto é ponto de mínimo local!
E pro outro ponto:
Logo, o ponto é ponto de sela!
Passo 5
(b)
Queremos os pontos de mínimo e máximo de sobre o círculo . Com uma restrição desse tipo meu amigo, não tem erro, vamos de Lagrange!
Antes, só uma coisa: a equação de um círculo com centro em e de raio é , certo? Então esse círculo tem centro em , que nada mais é que o ponto , e tem raio . Vamos dar uma olhadinha nele:
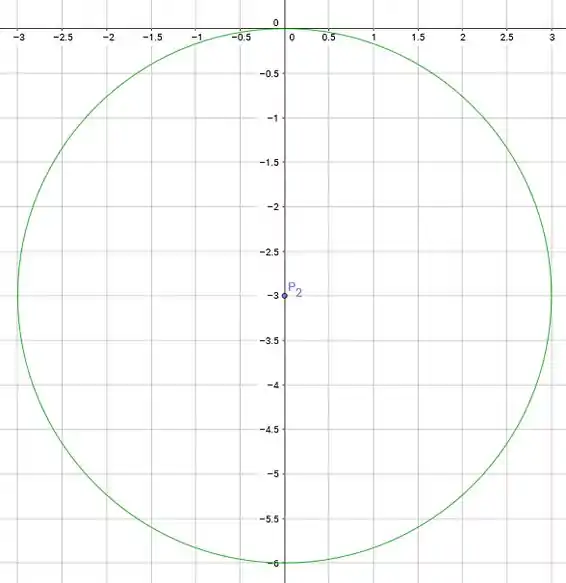
Passo 6
Show, agora vamos aplicar nosso passo a passo de questão de Lagrange!
Já temos o gradiente da , calculamos na letra (a):
Beleza, agora vamos pegar a equação do círculo e jogar tudo pro lado esquerdo, deixando na direita:
E vamos chamar o lado esquerdo dessa equação de :
Agora vamos calcular as derivadas parciais da :
E, usando a regra da cadeia:
Ou seja, o gradiente da é:
Passo 7
Excelente! Preparamos bem o terreno pros multiplicadores de Lagrange! Vamos ter:
Também temos a equação do círculo, então o nosso sistema vai ficar assim:
Passo 8
Bem, agora é arregaçar as mangas e partir pras contas!
Pela equação , temos:
Se :
A equação fica:
Beleza, vamos testar esses dois casos:
- Se na equação vamos ter:
- Se a equação vai ficar:
o que é impossível! Então vamos descartar a possibilidade .
Beleza! Achamos mais 2 pontos, e .
Passo 9
Ainda temos a outra possibilidade que a equação nos deu, lembra?
Se :
A equação fica:
Opa! Achamos mais 2 pontos: e .
Passo 10
Show, estamos quase acabando!
Como os pontos críticos de e que achamos na letra (a) não estão sobre o círculo, vamos ter apenas 4 candidatos a ponto de máximo e mínimo de sobre o tal círculo. São os pontos:
Saca só como eles ficam na figura:
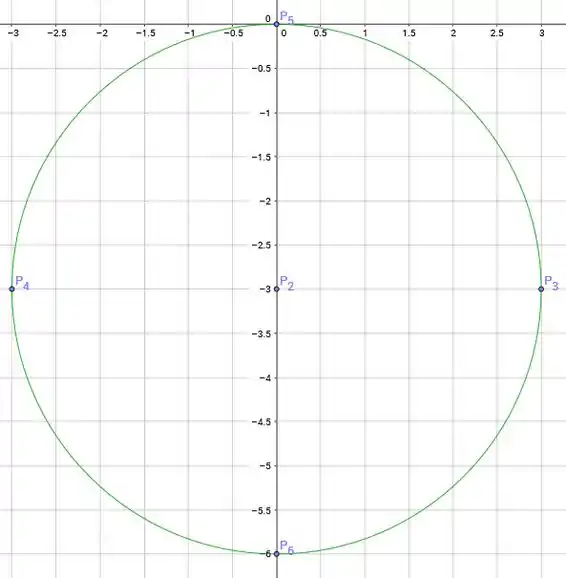
Beleza, então agora só resta calcular o valor da função em cada ponto e ver qual vai ser o máximo e qual o mínimo! Dá uma olhada nessa tabela:

Portanto, e são os pontos de máximo, enquanto é o ponto de mínimo!
Passo 11
(c)
Bem, agora queremos os pontos de mínimo e máximo de sobre o disco .
Opa! É a mesma equação do círculo, só trocando, o “” pelo “”. Ou seja, o disco vai ser assim:
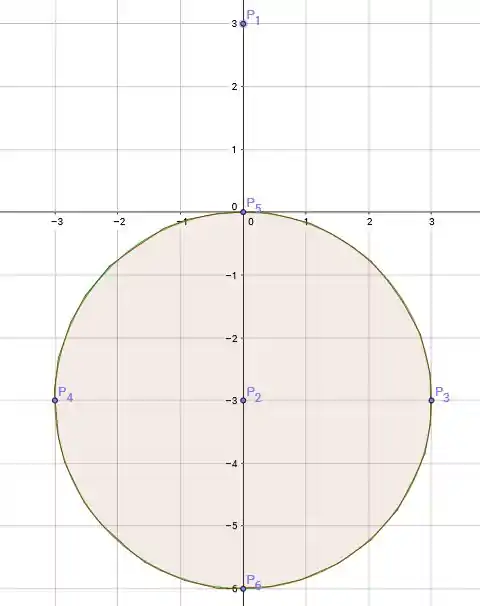
Repare que o ponto não está no disco, então nossos candidatos a ponto de máximo e mínimo são os outros pontos: e . Ou seja, são os mesmos candidatos que pro círculo, mais o ponto !
O valor máximo era 27, em e , e o valor mínimo era -18, em .
E
Ou seja:
Então vamos ter exatamente o mesmo resultado da letra (b): os pontos de máximo são e , com o valor máximo 27, e o ponto de mínimo é , com o valor mínimo -18.
Resposta
(a)
Os pontos críticos são (mínimo local) e (ponto de sela).
(b) e (c)
Pontos de máximo: e , com valor máximo .
Ponto de mínimo: , com valor mínimo .