Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Multiplicadores de Lagrange com 1 Restrição

Ver Teoria
Exercício 931234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768697071727374757677787980818283848586878889909192949596979899100

Enunciado

Seja f x , y = ( y 2 - x 2 ) 3

  1. Encontre e classifique os pontos críticos de f .
  2. Determine os pontos extremos globais de f em S = x ,   y ) ∈ R ; x 2 + y 2 ≤ 1

Passo 1

Letra a) A primeira coisa que temos que averiguar em um exercício como esse é justamente os pontos em que o gradiente se anula:

∇ f x , y = 0 ;   0

onde

∇ f x , y = ∂ f ∂ x x , y ,   ∂ f ∂ y x , y

Calculando essas derivadas parciais do vetor gradiente...

∂ f ∂ x x , y = - 2 3 x

∂ f ∂ y x , y = 2 3 y

Logo

∇ f x , y = ∂ f ∂ x x , y ,   ∂ f ∂ y x , y = - 2 3 x ,   2 3 y = ( 0 ,   0 )

Concluímos que o único ponto que crítico é

x = 0 ,   y = 0 ⇒ x ,   y = ( 0 ,   0 )

Passo 2

Para classificar esse ponto, vamos olhar para o teste da matriz Hessiana, que é aquela matriz contendo as derivadas de segunda ordem da função, se lembra? Dessa forma aqui

H = ∂ f 2 ∂ x 2 ∂ f 2 ∂ x ∂ y ∂ f 2 ∂ y ∂ x ∂ f 2 ∂ y 2

Calculando as derivadas parciais de segunda ordem, vamos encontrar

∂ f 2 ∂ x 2 = ∂ ∂ x ∂ f ∂ x = ∂ ∂ x - 2 3 x = - 2 3

∂ f 2 ∂ x ∂ y = ∂ ∂ x ∂ f ∂ y = ∂ ∂ x 2 3 y = 0

∂ f 2 ∂ y ∂ x = ∂ ∂ y ∂ f ∂ x = ∂ ∂ y - 2 3 x = 0

∂ f 2 ∂ y 2 = ∂ ∂ y ∂ f ∂ y = ∂ ∂ y 2 3 y = 2 3

Como essas derivadas não dependem de x e y , teremos que a matriz Hessiana, vai valer

H x , y = - 2 3 0 0 2 3

Para todos os pontos, em especial para o nosso único ponto crítico. Avaliando o determinante dessa matriz no ponto ( 0 ,   0 )

H 0 ,   0 = - 2 3 0 0 2 3 = - 4 9

Como o determinante da Hessiana é negativa, podemos então garantir que o único ponto crítico é de sela :)

Passo 3

Letra b)

Então... agora temos que determinar o máximo e mínimo da f não mais em todo o plano cartesiano e sim dentro de uma restrição, um conjunto restrito de pontos ( x ,   y ) dentro da superfície x 2 + y 2 ≤ 1 .

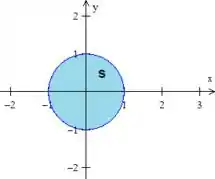
Como já sabemos, no interior dessa região, o único ponto que poderia ser de máximo e mínimo era a origem, mas... a gente já viu que não é! Logo, os máximos e mínimos só podem estar em cima da curva que delimita a região, a circunferência x 2 + y 2 = 1 .

Passo 4

Como a gente tem uma restrição podemos fazer essa busca utilizando multiplicadores de Lagrange, correto?

A nossa restrição, não está em função de 0 , mas não tem nenhum problema, pois passando o 1 para o outro lado na equação da restrição, vamos ganhar

x 2 + y 2 = 1 → x 2 + y 2 - 1 = 0

Agora a gente pode igualar esse lado direito a função g x ,   y = x 2 + y 2 - 1 e a gente obtém aquela nossa restrição g x ,   y = 0 que precisávamos em Lagrange, tá ligado?:)

Passo 5

Pois bem! Agora podemos aplicar Lagrange:

∇ f x ,   y = λ ∇ g x ,   y

Calculando o gradiente da g e lembrando que o da f é - 2 3 x ,   2 3 y

∇ g x ,   y = ( 2 x ,   2 y )

Logo teremos

∇ f x ,   y = λ ∇ g x ,   y ⇒

- 2 3 x ,   2 3 y = λ ( 2 x ,   2 y )

Igualando termo a termo e acrescentando a curva de restrição

- 2 3 x = 2 λ x 2 3 y = 2 λ y x 2 + y 2 = 1

Passando esses termos que contem λ para o outro lado e colocando em evidência, teremos o seguinte

- 2 x 1 3 + λ = 0 2 y 1 3 - λ = 0 x 2 + y 2 = 1

Se x e y nas equações acima não podem ser zero ao mesmo tempo devido à restrição da circunferência, então

- 2 x 1 3 + λ = 0 →   1 3 + λ = 0 → λ = - 1 3  

E

2 y 1 3 - λ = 0 → 1 3 - λ = 0 → λ = 1 3

Analisando x e y para esses valores de λ , vemos que

  • Quando λ = - 1 3 ,

    • x = 0 ⇒     0 2 + y 2 = 1     ⇒       y = ± 1

    Logo, ganhamos dois pontos pra teste aqui: ( 0 ,   1 ) e ( 0 ,   - 1 )

  • Quando λ = 1 3 ,

y = 0 ⇒     x 2 + 0 2 = 1     ⇒       x = ± 1

Logo, ganhamos mais dois pontos aqui: ( - 1 ,   0 ) e ( 1 ,   0 )

Passo 6

Analisando agora os pontos que encontramos na função f x , y = ( y 2 - x 2 ) 3 , vamos ganhar que devido ao quadrado em x e y

f 0 ,   1 = f 0 ,   - 1 = 1 3

E

f - 1 ,   0 = f 1 ,   0 = - 1 3

Portanto ( 0 ,   1 ) e ( 0 ,   - 1 ) são máximos globais, ( - 1 ,   0 ) e ( 1 ,   0 ) , mínimos globais.

Resposta

a) Ponto crítico: ( 0 ,   0 ) . Este ponto, é um ponto de sela.

b) Pontos de máximos globais: ( 0 ,   1 ) e ( 0 ,   - 1 )

Pontos de mínimos globais: ( - 1 ,   0 ) e ( 1 ,   0 )

Exercícios de Livros Relacionados

Cada um desses problemas de valor extremo possui uma solução com um valor máximo e um valor mínimo. Utilize os multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita
Determine os valores extremos de f sujeita a ambas as restrições. f x , y , z = x 2 + y 2 + z 2 , x - y = 1 , y 2 - z 2 = 1
Utilize os multiplicadores de Lagrange para dar uma solução alternativa aos exercícios da Seção 14.7 indicadosExercício 39
Utilize os Multiplicadores de Lagrange para determinar os valores máximo e mínimo da função sujeita à(s) restrição(ões) dada(s). f x 1 ,x 2 , … , x n = x 1 + x 2 + … + x n x 1 2 + x 2 2 + … + x n 2 =
(a) Se seu sistema de computação algébrica traça o gráfico de curvas definidas implicitamente, use-o para estimar os valores mínimo e máximo de f x ,y = x 3 + y 3 + 3 x y sujeita a x - 3 2 + y - 3 2 =