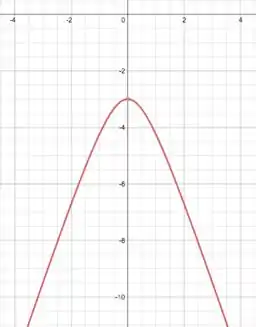
Esboce a imagem da seguinte curva plana:
Passo 1
Para encontrar a imagem dessa curva, a menos que você queira ficar marcando ponto para esboçar (só que não), devemos encontrar a equação cartesiana.
Como
Então
Passo 2
Agora, como fazemos para encontrar uma relação entre e ?
Bom, como temos tangente e secante, nada mais intuitivo que pensar primeiro em alguma equação que relacione essas duas funções!
Temos que:
Como e , podemos escrever:
Passo 3
Essa é a equação de uma hipérbole! Lembra como fazemos para esboçar uma?
Os vértices estão sobre a raiz quadrada do denominador da variável que tem o , e a “boca” aponta para a variável com o.
No nosso caso, temos a boca apontando para no sentido do eixo e os vértices em . Teremos algo assim:
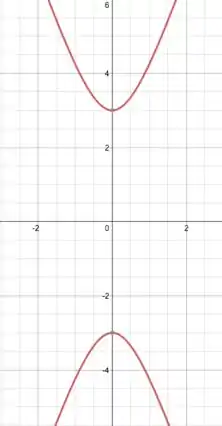
Passo 4
Mas temos que tomar cuidado com uma coisa! A função é restrita! Ele disse que varia entre e .
Nesse intervalo, temos a tangente variando entre (a partir de valores pouco maiores que e (que é atingido quando se aproxima de ). Além disso, a secante, que é , varia entre até , quando se aproxima de (e o passa a valer ).
Assim, o gráfico se restringe à parte de baixo da hipérbole, pois a parte do não atinge valores maiores que . Ficando então:
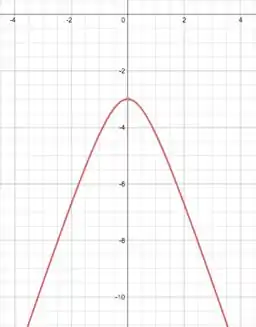
Resposta