Caso 1
O gráfico mostra o comportamento do módulo do campo magnético criado por um fio retilíneo cilíndrico muito longo como função da distância radial até seu eixo de simetria. Para , é linear. Para , a função é inversamente proporcional a .
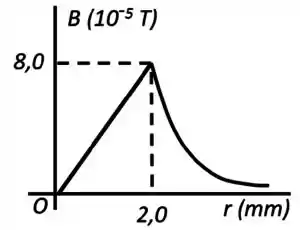
- A densidade de corrente é uniforme dentro do fio? Justifique a sua resposta cuidadosamente usando a lei de Ampère.
- Suponha, agora, que a corrente no fio sentido e que a densidade de corrente seja uniforme. Calcule o vetor , em .
- Em função de e , calcule a razão de modo que a força magnética resultante do fio sobre a espira seja nula.
Caso 2
Considere, agora, uma espira em forma de trapézio (figura abaixo), que tem dois lados paralelos entre si e também paralelos a um fio muito longo pelo qual passa uma corrente .
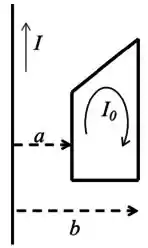
Pela espira circula uma corrente no sentido horário, mas seus lados não paralelos estão blindados do campo magnético causado pelo fio. O segmento da espira mais próximo ao fio e está à distância do fio, e o segmento mais distante mede e está à distância do fio.
Passo 1
a) Para respondermos este item, precisamos encontrar qual é o valor da densidade de corrente .
Na região dentro do cilindro, para a qual temos , o campo magnético tem comportamento linear. Por isso, podemos escrever esse campo como , o que mostra que ele só depende da componente radial , ou seja, tem simetria radial.
Para nos ajudar na desenvolvimento das contas, vamos olhar para a figura abaixo, que mostra o perfil do cilindro com a curva fechada (amperiana) de raio . Colocamos, para facilitar nossas contas, ambos os vetores densidade de corrente e a área entrando no cilindro e paralelos um ao outro.
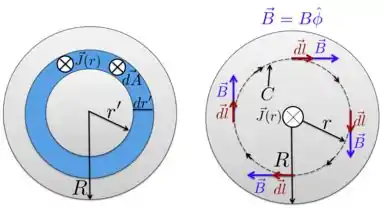
Além disso, a circunferência de raio orientada no sentido horário é a nossa amperiana, cujo vetor é paralelo ao campo em todos os pontos. Pela simetria, como vimos, esse campo depende apenas de e tem o mesmo valor em todos os pontos da amperiana.
Pausa para Sugestão: sempre tente identificar essas características do vetores no problema que você tiver resolvendo, porque isso te dá segurança na hora de aplicar a lei de Ampère. Beleza? Apesar do textão aí em cima, vale a pena ler essa parte com calma para fixar as ideias...
Passo 2
a) Continuação...
Depois desse passo (MUITO IMPORTANTE!!) de identificar as simetrias e os vetores envolvidos no problema, vamos juntar tudo e jogar dentro da lei de Ampère. Fazendo isso, temos:
em que é a corrente que atravessa a área delimitada e podemos calculá-la como:
já que é paralelo a .
Colocando essa expressão na lei de Ampère e lembrando para , temos:
Agora, vamos fazer o seguinte: derivar ambos os lados dessa última equação com relação a . Derivando o lado esquerdo primeiro, temos: . Moleza, né?
Seguindo e derivando o lado direito, que é uma função de escrita em termos de uma integral, obtemos que o resultado é o integrando () aplicado em , ou seja, . Isso que acabamos de fazer é o chamado “Teorema Fundamental do Cálculo”.
Igualando esses resultados, temos:
que mostra para nós que a função densidade de corrente tem o mesmo valor para todo , ou seja, é uma densidade de corrente uniforme.
Passo 3
b) Do gráfico que o problema dá, a gente vê que o coeficiente angular da reta é dado por:
Jogando na expressão que encontramos no final do Passo 1, obtemos:
O vetor densidade de corrente é, então,
Passo 4
c) Aqui no Caso 2, o campo magnético produzido pela corrente do fio infinito é perpendicular a ambos os fios de comprimento e e está entrando no plano da página. O que muda é a intensidade desse campo sobre cada um desses fios do trapézio.
No fio à distância de , o módulo do campo é:
e tem a mesma intensidade em toda a extensão de , e no ponto à distância de ,
que tem o mesmo valor em todo o comprimento .
Como a corrente tem sentido diferente nos fios e do trapézio, a força em cada um deles também tem a mesma direção, porém sentidos diferentes. Para que a força resultante no trapézio seja nula, os módulos dessas forças nos fios e devem ser iguais.
Portanto,
que simplificada, nos dá o seguinte resultado: