A Figura abaixo mostra quatro correntes iguais a e cinco linhas amperianas envolvendo estas correntes.
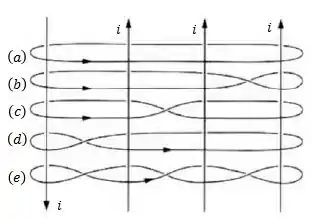
Calcule o valor da integral ao longo das curvas amperianas nas direções dadas.
Define-se densidade superficial de corrente elétrica a grandeza: , onde é a corrente e é a área da superfície considerada.
Considere agora um fio muito longo de seção circular e de raio onde passa uma densidade de corrente com direção paralela ao eixo central. O módulo desta densidade de corrente varia linearmente com o raio do fio de acordo com a equação , onde é uma constante. Determine, usando a lei de Ampere o campo magnético em .
Passo 1
Calcule o valor da integral ao longo das curvas amperianas nas direções dadas.
Quando o problema pede para calcularmos a integral , no fundo, ele tá implorando pra usarmos a lei de Ampère aqui, que é dada por:
Onde é a corrente envolvida pela amperiana.
Para saber se consideramos a corrente positiva ou negativa devemos levar em consideração o sentido da amperiana, usando a regra da mão direita.
Logo:
Passo 2
Considere agora um fio muito longo de seção circular e de raio onde passa uma densidade de corrente com direção paralela ao eixo central. O módulo desta densidade de corrente varia linearmente com o raio do fio de acordo com a equação , onde é uma constante. Determine, usando a lei de Ampere o campo magnético em .
A lei de Ampère é dada por:
Devido à geometria do problema, podemos simplificar essa expressão para:
Então, antes de encontrarmos o valor de , temos que encontrar uma expressão para a corrente.
Passo 3
Por definição, a corrente e a densidade de corrente estão associados por:
Logo:
Onde é um pedaço infinitesimal da área. Portanto, fazendo as substituições, teremos:
Passo 4
Voltando ao problema, já tínhamos concluído que, de acordo com a lei de Ampère, o campo magnético é dado por:
Onde:
Substituindo na expressão de , teremos:
Agora tá bonito. O problema pediu para calcularmos o campo magnético para , logo:
Onde:
Substituindo na expressão de , teremos:
Resposta