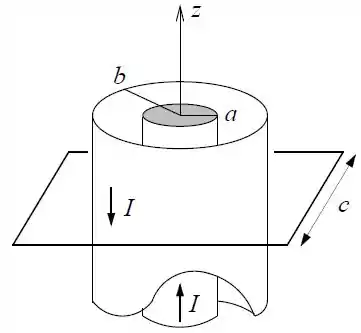
Um fio condutor cilíndrico muito longo e de seção reta de raio está envolto por uma casca cilíndrica condutora fina de raio , formando um cabo coaxial cujo eixo coincide com o eixo . Pelo fio passa uma corrente , na direção positiva do eixo , uniformemente distribuída através de sua seção reta. Na casca cilíndrica passa uma corrente total , na direção negativa do eixo , conforme a figura.

Calcule o vetor campo magnético nos pontos onde ( é a distância do ponto até o eixo ).

Calcule o vetor campo magnético na região .

Calcule a integral ao longo do quadrado de lado coaxial com o eixo , conforme a figura.

Calcule o vetor campo magnético nos pontos onde ( é a distância do ponto até o eixo ).

Opa! Molezinha, hein!

Pra calcular o campo magnético, basta usar a Lei de Ampère:

Dada a geometria cilíndrica do problema, onde a nossa amperiana será uma circunferência de raio , podemos simplificar a Lei de Ampère:

Como a corrente está no sentido positivo do eixo , usando a regra da mão direita, vemos que o vetor campo magnético será o seguinte:

Onde é positivo no sentido anti-horário.

O nosso único problema aqui é determinar , mas como o problema disse que a corrente está uniformemente distribuída ao longo da seção reta do fio, basta usar uma regra de três pra facilitar a nossa vida:

Substituindo de volta na expressão que encontramos para o campo magnético: