UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Profº Otoniel Nogueira - Lista 08, Questão 8
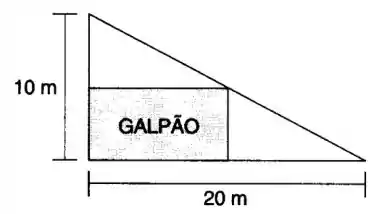
Um galpão retangular deve ser construído num terreno com a forma de um triângulo, conforme a figura a seguir. Determinar a área máxima possível para o galpão. Utilize o método dos multiplicadores de Lagrange.
Passo 1
Eaee!!! Belezinha? Bom... a questão quer que calculemos a área máxima possível para o galpão mostrado na figura abaixo utilizando o método dos multiplicadores de Lagrange.
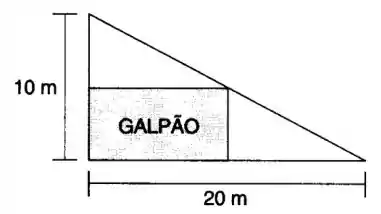
Para isso, primeiramente devemos determinar a nossa função e a restrição.
A nossa função é a área do galpão, que é dada por:
E a nossa restrição é aquele cantinho do galpão que toca no triângulo.
Se colocarmos a nossa figura em coordenadas cartesianas, obtemos:
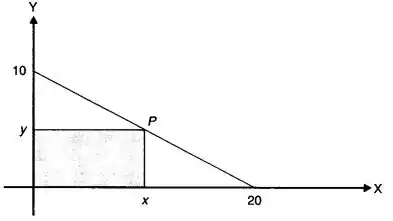
Logo, percebemos que a hipotenusa do nosso triângulo é uma reta com a seguinte equação:
Que é a nossa restrição (já na forma de colocarmos em Lagrange hehe).
Agora vamos descobrir a nossa área máxima utilizando os multiplicadores de Lagrange!!
E aí? Bora lá?
😉
Passo 2
Então... a função lagrangeana é dada por:
Derivando em relação às três variáveis, temos:
Nesse sentido, igualando as derivadas a zero, obtemos:
Resolvendo o sistema, encontramos e .
Portanto, substituindo esses pontos na função, obtemos a nossa área:
Entendeu direitinho? Responde aee ;)
Resposta