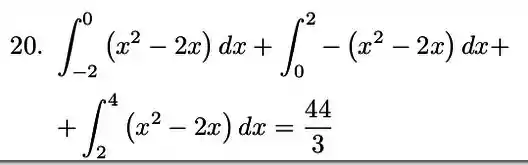Passo 1
Olha aqui como fica o gráfico com essas curvas.
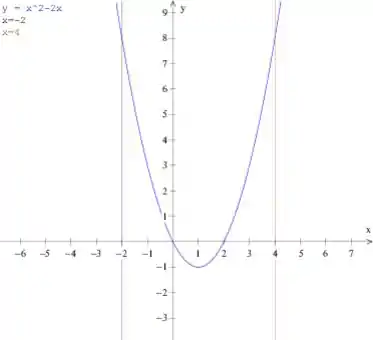
O objetivo aqui é encontrar a área entre a curva e as duas retas e .
Passo 2
Vamos começar encontrando as raízes da equação da curva para achar os limites da nossa região.
Passo 3
Agora vamos montar as nossas integrais para calcular a área, observando as regiões do nosso interesse, ou seja, entre a curva e as retas do problema. As raízes que achamos no passo anterior vão fazer parte dos nossos limites de integração.
Passo 4
Montado nosso problema, só falta integrar. Vamos lá!
Pronto, encontramos a área da região.
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x